Уравнение Шредингера для атома водорода имеет вид:
,
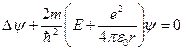где m — масса электрона, E — полная энергия электрона в атоме. В записанном уравнении используется потенциальная энергия кулоновского взаимодействия электрона с ядром в виде 
, где r — расстояние между электроном и ядром.
Состояние электрона в атоме водорода описывается волновой функцией
yn,l,m (r,q,j), которая является решением записанного уравнения Шредингера в сферических координатах r,q,j. Эта волновая функция зависит от трех квантовых чисел: главного (n), орбитального (l) и магнитного (ml). Главное квантовое число ( n = 1, 2, 3,…) определяет значения энергии электрона на энергетическом уровне
.
Формулу, определяющую энергию электронов, можно называть условием квантования энергии.
Орбитальный механический момент (момент импульса) электрона также квантуется, т.е. принимает дискретные значения:
,
где l – орбитальное квантовое число; l = 0, 1,…, (n - 1). Состояния с l = 0 называются s-состояниями электрона, l = 1, 2,3,..соответственно называются p, d. f,.. состояниями.
Проекция вектора 
на направление внешнего магнитного поля также принимает дискретные значения: 
, где ml – магнитное квантовое число, которое может принимать значения ml = 0, ±1, ±2,…, ±l. Магнитное квантовое число (ml) определяет проекцию момента импульса электрона на заданное направление.
Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве.
Энергетические уровни называются вырожденными, если одинаковым значениям энергии соответствует несколько волновых функций с различными квантовыми числами (вырожденные состояния).
Кроме орбитального механического момента электрон также обладает собственным механическим моментом 
, называемым спином, и соответствующим ему собственным магнитным моментом 
. Значение спина квантуется по закону:
,
где s – спиновое квантовое число. Проекция спина на направление внешнего магнитного поля, определяется выражением:
,
где ms – магнитное квантовое число, оно может иметь только два значения (ms = ±1/2).
Наличие спина у электрона не следует из решений уравнения Шредингера.
Решение уравнения Шредингера дает более полное описание атома водорода, чем теория Бора. В отличие от теории Бора, квантовая механика позволяет рассчитать состояния всех атомов таблицы Д.И.Менделеева.