Пусть (X, £) – конечное частично упорядоченное множество. Рассмотрим последовательность функций Pn: X ´ X® Z, определенных при n = 0 и n = 1 по формулам:
![]()
![]()
а при n ≥ 2 по формуле:
Pn(x,y) = |{( x1, x2, …, xn-1): x< x1 < x2 < … < xn-1 <y}|.
Определение 1
Функцией Мебиуса m: X´X®Z называется функция, определенная по формуле:
![]() .
.
Определение 2
Пусть X = {x1, x2, …, xn} – конечное частично упорядоченное множество, матрицей смежности называется матрица A, имеющая коэффициенты:
![]()
Лемма 1
Пусть X = {x1, x2, …, xn} – конечное частично упорядоченное множество, A – матрица смежности. Тогда матрица M, коэффициенты которой равны значениям m(xi, xj), будет обратной к матрице A.
Доказательство
Пусть Id – единичная матрица. Положим Q = A - Id. Тогда A = Id + Q. Откуда
A-1 = Id - Q + Q2 - Q3 +×… = ![]() .
.
Легко видеть, что коэффициенты матрицы Qk равны Pk(xi,xj), откуда
![]() ,
,
в силу
![]() .
.
Что и требовалось доказать.
Пример
X = [n].
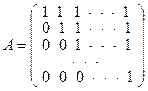 ;
; 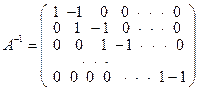 .
.
Отсюда получаем
m(i,i) = 1; m(i,i + 1) = -1.
Остальные значения функции Мебиуса равны 0.