Естественная дедуктивная система – основная система выводов в логике предикатов, в которой функционируют как единое целое группы правил вывода и логические аксиомы. В системе с малым числом правил вывода обычно имеется большое число логических аксиом, и наоборот.
Система логических исчислений LK
а) Пусть имеются формулы А1, …, Аm ® B1, …, Bn, где m, n ³ 0.
В LK используют представление называемое секвенцией:
А1, …, Аm ®B1, …, Bn, где m, n ³ 0.
А1, …, Аm – антецедент.
B1,…, Bn – сукцедент.
Если при m, n ³ 1 выполняется А1 и … и Аm, то справедливо B1 или … или Bn.
А1 Ù … Ù Аm É B1 Ú …Ú Bn
Если m = 0, то B1 Ú …Ú Bn – истина.
Если m = 0, то А1 Ù … Ù Аm – ложь.
@ ( ® B1, …, Bn) – среди Bi есть по крайней мере одно правильное логическое выражение. Формула: B1 Ú …Ú Bn.
(A1, …, Am ® ) @ набор A1, …, Am является противоречивым. Формула ØA1, …, ØAm.
A, B, C, D, … – формулы.
G, D, Q, P, … – ограниченный Ú 0 ряд формул.
б) LK – аксиома — это секвенция вида C ® С, где С — произвольная формула.
Логические и структурные правила вывода
Существует девятнадцать правил вывода в системе LK. Из секвенции над чертой выводится секвенция под чертой @.
Если справедлива верхняя, то справедлива нижняя. Над чертой располагается первая или вторая секвенция. Правила вывода имеют имена, которые заключаются в скобки слева от правила.
Секвенции делятся на логические (а) и структурные (б).
а) Может быть только один логический символ в нижней секвенции. Делятся на два типа:
а1) логический символ стоит после стрелки;
а2) логический символ стоит перед стрелкой.
Имя правила показывает его тип (Ù® — Ù перед стрелкой в нижней секвенции). В этих правилах х – переменная; t – терм.
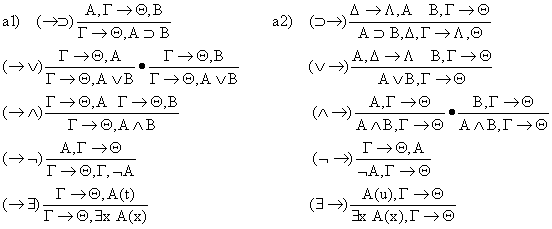
Связная переменная – если х появляется в области действия " х Ú $ x или если х присутствует в " х Ú $ x.
Например:
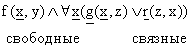
Правило: среди всех свободных переменных, вместо которых подставляется терм t, не может возникнуть ни одной связной.
Для $® и ®". В этих правилах:
u – переменная;
А(а) – результат подстановки u вместо x в формуле A(x)
u — не появляется в нижней секвенции.
u — собственная переменная правила вывода.
![]()
б) T – сокращение (Thinning)
C – противоречие (Contradiction)
I – взаимный обмен (Interchange)
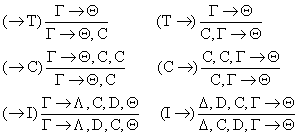
Это правило необходимо для перемещения формулы до соответствующей позиции.
Правило сечения:
![]() .
.
Понятия противоречивости, достоверности и выполнимости
Пусть знания представлены формулами и A1, …, Am последовательность этих формул.
Чтобы проверить, можно ли на основе этих знаний вывести новый факт В, представленный формулой, и проверить возможность существования доказательства Г® B.
Если доказательство существует, то выражение Г® В доказуемо и записывается в следующем виде: |-Г® B.
В доказуемо на основании Г (Г |- В). Если Г = 0 (m = 0), то |- B (В – доказуемо). Таким образом, запись |- Г® означает, что Г – противоречивая последовательность, в остальных случаях Г – непротиворечиво.
Из противоречивых знаний можно вывести любой факт.
Интерпретация секвенции
Секвенция интерпретируется как формула. Постоянные, предикатные и функциональные символы используются для описания некоторого мира. Их интерпретация может быть любой. Пусть существует S – секвенция, определить ее I — интерпретацию с1, …, сk – const, Î S; f1, …, fm – функциональные символы; p1, …, pn – предикатные.
Универсум (u) – множество всех индивидуумов, которые являются структурными элементами описываемого в данный момент мира.
u – произвольное непустое множество. ci (1 £ i £ k) интерпретируются как имена, идентифицирующие элементы, принадлежащие u. Для определения I необходимо определить, какой элемент идентифицирует k " const ci. Если I определено, то все термы, не имеющие переменные в S, можно интерпретировать как элементы множества u. Атомы, не имеющие переменных, определяются истиной или ложью в I.
Если есть переменные, то всякий атом определяется истиной или ложью и происходит замена на интерпретацию логического символа.
Интерпретация логического символа не зависит от частной интерпретации I.
Пусть x1, …, xm – свободные переменные S.
Если "x1, …, "xm S в I, являющемся t, то S достоверна в I.
Если $x1, …, $xm S — в I = t, то S выполнима в I.
Если S достоверна во всех I, то она называется общезначимой.
S выполнима в том случае, если она выполнима в I.
Теорема о полноте
Если S доказуема, то она достоверна.
Если S достоверна, то она доказуема
Это означает, что для доказательства в системе выводов логики предикатов в проверке всех секвенций не требуется других правил вывода.
Теорема о неполноте Геделя–Росса: Если Г содержит аксиомы математической логики и является непротиворечивой, то существует формула А, не содержащая свободных переменных, такая, что оба приведенных выше утверждения не выводимы.
Под аксиомами математической логики понимаются аксиомы, относящиеся к свойствам множества {0, 1, 2, … }, т.е. если ![]() ¹ x и
¹ x и ![]() =
= ![]() , то x = y; x + 0 = x. Здесь
, то x = y; x + 0 = x. Здесь
![]() – следующее после x число.
– следующее после x число.