Программа сначала «засоряется» некоторым количеством известных ошибок,    которые вносятся случайным образом. Затем делается предположение, что для собственных ошибок программы и внесенных ошибок вероятность обнаружения при по-следующем тестировании одинакова и зависит только от их количества. Программа тестируется в течение некоторого времени, собственные и внесенные ошибки от-сортировываются. Первоначальное число ошибок (N) оценивается по следующей формуле:

,

где s – число ошибок, внесенных в программу;   n – число найденных при тестировании собственных ошибок программы;             v – число найденных внесенных ошибок.

Например, если в программу внесено 20 ошибок и к некоторому моменту тестирования обнаружено 15 собственных и 5 внесенных ошибок, значение N можно оценить в 60.

Значение N можно оценивать после обнаружения каждой ошибки, Миллс предлагает во время всего периода тестирования отмечать на графике число найденных ошибок и текущие оценки для N.

Вторая часть модели связана с выдвижением и проверкой гипотезы об N. Пусть в программе имеется не более k собственных ошибок и пусть внесено в нее еще s ошибок. Программа тестируется, пока не будут обнаружены все внесенные ошибки, подсчитывается число обнаруженных собственных ошибок.

Уровень значимости:

.

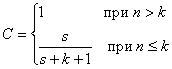Величина С является мерой доверия к модели. Например, утверждается, что в программе нет ошибок (k = 0), вносится 4 ошибки в программу, при тестировании все они обнаруживаются и при этом не находятся собственные ошибки программы, тогда  C = 0.8. Чтобы достичь уровня 95 %, необходимо было бы внести в программу 19 ошибок.

Слабость второй формулы в том, что нельзя предсказать величину С до тех пор, пока не будут обнаружены все внесенные ошибки. Недостаток модели состоит в предположении, что для собственных и внесенных ошибок вероятность обнаружения одинакова.