Можно выделить два подхода к модификации топологии нечеткой нейронной сети на этапах обучения и использования. Первый, традиционный подход основан на введении дополнительных продукционных правил в базу знаний системы. При этом следует учитывать непротиворечивость ее пополнения.

Другой подход предполагает генерацию новых продукционных правил, не противоречащих правилам из базы знаний системы, исходя из анализа экспериментальных данных об объекте на основе процедуры, рассмотренной ниже.

Предположим, что исследуемый объект имеет n входов (иначе, векторный вход ) и один выход y и имеет «истинное» (неизвестное) описание:

где  – функция неизвестного вида; – случайная аддитивная помеха (отражающая действие не учитываемых факторов) с нулевым средним значением и произвольным (неизвестным) распределением на .

Предположим далее, что на объекте может быть реализован эксперимент, заключающийся в регистрации  пар значений  при этом величины (векторы)  измеряются без ошибок; значение  при необходимости допускает модификацию.

Алгоритм построения системы может быть теперь описан следующим образом.

Шаг 1. Из m (m<N) произвольных значений  составляется начальная база знаний модели, отображаемая матрицей  со строками вида

.

Такое представление, очевидно, эквивалентно набору продукционных правил вида:

.

Шаг 2. Для каждой новой экспериментальной точки <> рассчитывается прогнозируемое значение по формуле, соответствующей рассмотренному центроидному методу:

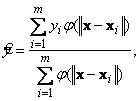
где  – функция колоколообразной или экспоненциальной формы:

Здесь  – параметр функций.

Шаг 3. Проверяется неравенство

где d – заданная константа, определяющая погрешность аппроксимации.

При выполнении неравенства база знаний системы пополняется путем расширения матрицы U (добавлением строки ). В противном случае матрица U остается без изменений.

Шаг 4. Проверяется правило останова. В данном варианте алгоритма построение модели считается законченным, если в соответствии с шагами 2 и 3 перебраны все N экспериментальных точек (без учета значений начальной базы знаний).

Если не все экспериментальные точки использованы, то осуществляется переход к шагу 2, в противном случае – останов.

В процессе реализации алгоритма параметры  и d считаются априори заданными.

При использовании системы заданными считаются матрица U (на этапе использования модели она не изменяется), отмеченные параметры  и d, и расчет  производится в соответствии с шагом 2 приведенного алгоритма.

Нетрудно видеть, что описанный алгоритм, в сущности, соответствует упрощенному алгоритму нечеткого логического вывода (см. подраздел 4.6), но отличается от последнего тем, что база знаний не остается фиксированной, а модернизируется по мере поступления экспериментальных данных. Причем непротиворечивость нового продукционного правила относительно набора правил из базы знаний гарантируется предложенной процедурой ее пополнения.