Важным достоинством моделирования происшествий с помощью диаграмм типа "дерево" является, как указывалось выше, возможность обстоятельного анализа интерпретируемых им процессов. Вот почему после построения деревьев происшествия и его исходов обычно приступают к проверке их адекватности исследуемым опасным процессам, а затем к качественному и количественному анализу полученных семантических моделей.

Правила определения событий. Определение всех событий рассматриваемых здесь моделей (каждой предпосылки дерева происшествия и каждого исхода дерева событий) следует проводить лишь через наиболее существенные признаки.

Прежде всего, для них необходимо указывать:

1) родовую принадлежность, например, "гибель, увечье, временная потеря трудоспособности человека" – для различных исходов несчастного случая или "отказ, ошибка, нерасчетное внешнее воздействие" – для предпосылок к нему;

2) межвидовые отличия внутри рода соответственно "по причине удара или захвата человека движущими частями, ингаляции или адсорбции вредного вещества" и "вследствие износа, усталости, стихийного бедствия".

В наименовании всех предпосылок и исходов каждой рассматриваемой здесь модели нужно избегать использования неясных слов и так называемых ошибок типа "круг в определении", т.е. попыток выразить содержание определяемых понятий через самих себя (например, "потребность – это то, в чем нуждаешься, а нужда – то, что требуется"). Наконец, для выявления причинно-следственных связей между событиями диаграмм типа "дерево" следует руководствоваться принятыми в формальной логике методами: единственного сходства, единственного различия и их комбинацией, а также методами остатков и сопутствующих изменений /8/.

Проверка правильности и полноты определения событий, учитываемых в диаграммах типа "дерево", позволяет приступить к их качественному анализу. Его основные задачи состоят в выявлении закономерностей возникновения и снижения ущерба от происшествий, т.е. в установлении, например, тех цепочек событий соответствующего дерева, реализация которых приводит к появлению либо к непоявлению его головного события, а также в количественной оценке вклада интересующих нас событий-предпосылок.

Рассмотрим последовательно особенности качественного анализа каждого рассматриваемого нами дерева.

Анализ дерева происшествия с помощью минимальных сочетаний. Наиболее удобны для качественного анализа дерева происшествия так называемые "минимальные сочетания предпосылок", под которыми подразумевается минимально необходимое и достаточное для достижения конкретного результата их множество. Естественно, что нас интересуют два результата: возникновение и предупреждение происшествий. Поэтому ниже будем иметь дело с двумя типами минимальных сочетаний – пропускным (аварийным) и отсечным (секущим).

Первое из них – минимальное пропускное сочетание (МПС) включает в себя наименьшее число тех исходных предпосылок дерева происшествия, одновременное появление которых достаточно для возникновения головного события (прохождения сигнала до него). Напротив, минимальное отсечное сочетание (МОС) формирует условия непоявления головного события. Это сочетание состоит из исходных событий

рассматриваемого дерева, гарантирующих отсутствие происшествия, при условии невозникновения одновременно всех входящих в него событий-предпосылок. Особенностью обоих типов минимальных сочетаний служит то, что они теряют присущие им свойства при удалении из каждого такого сочетания хотя бы одного события.

Примеры. Для иллюстрации качественного анализа моделируемых опасных процессов с помощью минимальных пропускных и отсечных сочетаний, воспользуемся деревом происшествия, изображенным на рис. 5.2.

На рис. 5.2 показаны условия возможного поражения человека электрическим током.

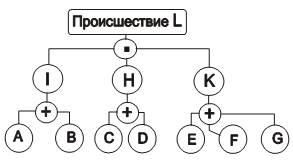
Рис. 5.2. Дерево происшествия

Предполагается, что головное для этой модели событие L явилось результатом одновременного наложения трех предпосылок: 1) появления потенциала высокого напряжения на корпусе электроустановки (H); 2) нахождения человека на токопроводящем основании (I) и 3) его прикосновения к этому корпусу (K).

В свою очередь, событие I явилось следствием возникновения любого из двух других исходных событий-предпосылок A и B, например, снижения сопротивления изоляции или касания токоведущими частями электроустановки ее корпуса по причине их раскрепления. Другое событие верхнего (промежуточного) уровня H также могло быть обусловлено двумя исходными предпосылками: C – нахождением человека на металлическом полу или D – его касанием заземленных элементов здания; а событие K – следствием одной из трех предпосылок E, F и G, например, необходимостью ремонта, технического обслуживания или использования электроустановки по прямому назначению.

Заметим, что данная модель может имитировать условия появления и другого происшествия, в частности – воспламенения паров водорода, выделяющихся из свинцовых аккумуляторов. Предпосылками промежуточного уровня в этом случае могут быть: H – накопление этого газа в аккумуляторной станции, I – отсутствие вентиляции данного помещения и K – появление внутри него источника воспламенения. В свою очередь, первая предпосылка – следствие длительного заряда неисправных аккумуляторных батарей (A) или отказа зарядных устройств (B); вторая – поломки вентиляторов (C) или закрытия воздуховодов (D); третья — искрения электрооборудования (E), появления людей с открытым огнем (F) или их курения (G).

В действительности (что подтверждается и анализом данной модели), одно дерево происшествия может иметь несколько минимальных сочетаний предпосылок, необходимых и достаточных для реализации или недопущения нежелательного головного события. Среди них могут быть МПС и МОС, состоящие только из одного исходного события – синглеты, из двух – дуплеты, из трех и более событий-предпосылок – (триплеты).

Так, например, в модели, приведенной на рис. 5.2, имеется 12 минимальных пропускных сочетаний исходных событий-предпосылок: триплеты – АСЕ, АСF, ACG, AДE, AДF, AДG, BCE, BCF, BCG, BДE, BДF, BДG и три минимальных отсечных сочетания таких событий: дуплеты – АВ, СД и триплет EFG.

Анализ значимости и критичности событий. Для отражения вклада конкретных предпосылок и их сочетаний в появление и предупреждение головного события дерева происшествия вводятся показатели их значимости или критичности. Эти категории могут использоваться для определения приоритетности осмотра, технического обслуживания и профилактики неисправностей того технологического оборудования, которое является причиной появления более значимых отказов, а также указывать на необходимость тщательного контроля соответствующих алгоритмов деятельности персонала или параметров рабочей среды. Не менее важны результаты оценки значимости и критичности всех предпосылок при коррекции и оптимизации проектируемых изделий и технологий.

Оценка значимости любого события основана на учете логики его объединения с другими предпосылками модели: чем ближе к ее вершине ощущается реализация события, тем больше его вклад в условия формирования головного происшествия. Например, в модели рис. 5.1, а более значима исходная предпосылка 1, так как ее появление доводит сигнал по левой ветви выше, чем событие 7. Напротив, предпосылка 7 более важна для предупреждения моделируемого происшествия, поскольку это достигается не появлением ее одной. Заметим, что в отличие от данной модели все исходные предпосылки рис. 5.2 одинаково значимы на качественном уровне.

В настоящее время также используются количественные критерии оценки значимости и критичности, обычно характеризующие вероятность или ожидаемое число наступлений головного события на некотором интервале времени. Как правило, одни из них указывают на изменение этих параметров вследствие появления либо непоявления конкретных исходных предпосылок и образуемых ими минимальных сочетаний, дру-гие – на ожидаемое среднее число происшествий, обусловленных такими событиями и их совокупностями за конкретный период.

Самым предпочтительным (среди известных ныне показателей значимости) считается критерий Фусселя-Везели /9/, измеряемый вероятностью того, что конкретное исходное событие или минимальное сочетание предпосылок дерева происшествия способствуют появлению его головного события.

Значение этого критерия  Ii^FV, определяемое при условии невозникновения исследуемого происшествия до момента реализации исходной предпосылки или сочетания, рассчитывается по следующим формулам:

;   

где P_i(t), Q(t) – вероятности наступления предпосылок и возникновения головного события дерева происшествий за некоторое время t; Р_k*(t), n – вероятности событий, принадлежащих конкретному минимальному сочетанию, и число таких событий в этом сочетании.

Известны и другие показатели, используемые для оценки значимости исходных событий и образуемых ими причинных цепей предпосылок к происшествию. В частности: а) Бирнбаума I_i^В, рассчитываемый либо взятием частной производной от Q(t) по P_i(t), либо как разность между вероятностями головного события до и после появления интересующих нас событий или их подмножеств; б) Барлоу-Прошана I_i^ВР, равный среднему числу происшествий, ожидаемому из-за возникновения оцениваемых нами исходных предпосылок.

Применимость критериев значимости. Основной интерес критерии значимости и критичности исходных предпосылок представляют для выбора первоочередных мероприятий по предупреждению происшествий. При прочих равных условиях наибольшую эффективность или экономию средств обеспечивают те из них, которые воздействуют на самые значимые и критичные события. В частности, из рис. 5.1, а нетрудно видеть, что снижение вероятности появления исходных предпосылок 1 и 7 на одну и ту же относительную величину окажется менее значимым для второй из них – за счет перемножения ее (меньшего единицы) параметра на такие же значения вероятностей других (соседних с событием 7) предпосылок.

Говоря об особенностях оценки значимости и критичности элементов дерева происшествия, следует обратить внимание также на корректность использования двух последних количественных критериев, иногда дающих неправдоподобные рекомендации. Дело в том, что их значения зависят не только от вероятности предпосылок, но и от способа их соединения логическими условиями данного дерева. Поэтому могут быть ситуации (например, при коротких интервалах времени работы хорошо резервированных технических систем), когда большую значимость вначале имеют самые надежные их элементы, а затем – менее надежные.

Дополнительную информацию об особенностях практического применения известных критериев оценки значимости и критичности можно обнаружить в работе /10/. Примеры качественного анализа дерева происшествия с помощью минимальных сочетаний каждого типа и рассмотренных выше показателей значимости приведены в главе 4.

Особенности анализа дерева исходов. Приступая к качественному анализу дерева событий – исходов происшествия, заметим, что, к сожалению, до сих пор не разработаны исчерпывающие рекомендации, пригодные для обстоятельного проведения такого анализа. По крайней мере, нам не известны такие, столь же конструктивные процедуры, как только что рассмотренные для предыдущей модели. Поэтому ниже мы ограничимся лишь изложением правил проверки полноты и качества выделения событий этого дерева, а также приведем более общие рекомендации по уточнению их признаков.

Во-первых, особое внимание необходимо обращать на то, чтобы события каждого уровня дерева исходов происшествия в совокупности представляли полную группу несовместных событий.

Из этого следует, что при построении данного дерева следует учитывать все возможные варианты: 1) истечения {1, 2,…i,…,l}, 2) трансформации и распространения {1,2,…,j,…,m}, 3) разрушительного поглощения {1, 2,…,k,…,n} потоков энергии и вещества, высвободившихся в результате происшествия. Иначе говоря, сумма безусловных вероятностей (Р) появления всех событий на каждом из трех уровней дерева исходов происшествия должна составлять единицу:

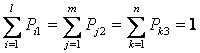.              (5.1)

Во-вторых, все события данного дерева и входящие в него ветви, воспроизводящие условия причинения ущерба людским, материальным и природным ресурсам, должны быть разделены между собой в соответствии с правилами деления понятий, принятыми в формальной логике.

Это означает, что возможные исходы должны делиться следующим образом: а) всегда по одному основанию, т.е. с соблюдением лишь одного признака деления на i, j и k-м уровнях дерева; б) непрерывно – переход к новому признаку может осуществляться лишь после рассмотрения всех возможных вариантов данного уровня;

в) соразмерно – суммарное число событий-исходов, выделенных на каждом уровне, должно быть точно равно их возможному количеству (в противном случае деление будет либо неполным, либо избыточным); г) с соблюдением требования непересекаемости различных исходов (учет конкретного события на данном уровне исключает возможность его повторного использования на этом же уровне) /11/.

В заключение отметим, что лишь использование вышеперечисленных рекомендаций, касающихся порядка построения и качественного анализа исследуемых здесь деревьев, может гарантировать адекватность реальности моделируемых ими опасных процессов, а также истинность выявленных при этом закономерностей появления и предупреждения происшествий. В свою очередь, без соблюдения таких условий нельзя обеспечить в последующем ни требуемой достоверности прогноза техногенного риска, ни точной оценки эффективности мероприятий по его уменьшению.