Вышел старик на берег моря. Стал он кликать золотую рыбку. Приплыла к нему рыбка и молвила человеческим голосом… Знакомая всем с детства сказочная фантастическая ситуация. А так ли уж она фантастична? Мог старик выйти на берег моря? Да, конечно. Вот мы и отняли от исходной ситуации (Ф) реальную часть (Р1):

Ф = Ф1+Р1.

Мог старик позвать рыбку? Да, мог. Вот еще одной реальной частью стало меньше:

Ф1 = Ф2 + Р2.

Но уже остальное кажется (Ф2) совсем фантастикой. Но ведь рыбка могла приплыть к берегу случайно (РЗ) и даже могла оказаться золотой (Р4). Но могла ли она заговорить человеческим голосом? Известно, что многие рыбы могут издавать звуки (Р5). Подобный анализ фантастической ситуации можно вести до тех пор, пока не найдется чисто фантастический остаток.

Метод золотой рыбки (МЗР) противоположен методу снежного кома и является применением системного подхода для последовательного анализа фантастических ситуаций.

Техника работы по МЗР:

· выбрать фантастическую ситуацию;

· последовательно, снимая с ситуации слои реальности, выявить исходную фантастическую идею, лежащую в ее основе.

Рекомендуется снимать с ситуации реальные составляющие небольшими слоями, постепенно. Получив исходную фантастическую идею, можно провести с ней работы по МСК, получая ряд других фантастических ситуаций.

При решении технических задач МЗР помогает выделить из сложной технической ситуации собственно изобретательскую задачу. При этом техника работы по методу выглядит так:

· в качестве фантастической выбирается ситуация, когда проблема как-то решена (как — неизвестно);

· снимая с фантастического решения слои реальности, получим чисто фантастический остаток, который и будет являться сутью задачи.

Иногда такой анализ исходной ситуации приводит прямо к решению задачи.

Примеры работы по МЗР

Пример 1. Рассмотрим ситуацию из повести А. и Б. Стругацких «Понедельник начинается в субботу». У героя в кармане один пятак. Он подходит к газетному киоску, кладет пятак на блюдечко, забирает газету и 3 копейки сдачи. Но, отойдя от киоска, Привалов обнаруживает в кармане, кроме трехкопеечной монеты, тот самый пятак, который он оставил в киоске.

Ситуация совершенно фантастическая, но если снять все очевидные слои реальности, то окажется в ее основе лежит идея неразменного пятака.

Пример 2. Бедный арабский юноша Аладдин взял старую медную лампу, потер ее, раздался хлопок и … перед ним возник могущественный джинн. Это ситуация Ф. Ясно, что Аладдин мог взять лампу (Р1) и потереть ее (Р2). А что же дальше? В результате трения лампа нагрелась, и газ вытолкнул пробку из лампы — хлопок (РЗ). А поскольку газ был дурманящий, то бедному суеверному юноше мог привидеться не только джинн, а что-нибудь и пострашнее.

В исходной фантастической ситуации под микроскопом МЗР не оказалось ничего фантастического.

Пример 3. Как защитить суда на подводных крыльях от кавитации, разрушающей крылья?

Исходная фантастическая ситуация (Ф): кавитация не разрушает подводные крылья.

Кавитация что-то разрушает (Р1), но крылья при этом остаются целыми (Ф1).

Крылья можно закрыть защитным слоем (Р2), но тогда этот слой должен быстро восстанавливаться (Ф2).

Восстановить защитный слой легко (РЗ), если он сделан из вещества, которого вокруг много, но слой должен наращиваться сам (ФЗ).

Вокруг подводного крыла вода (Р4), слой воды наращивается сам (Ф4). Как нарастить слои воды на крыло?

Такая формулировка задачи почти сразу же приводит к ответу: надо охлаждать подводное крыло, чтобы намораживать на нем защитный слой льда из окружающей воды.

Пример 4. Необходимо предложить способ измерения глубины реки с самолета. Представим задачу в виде фантастической ситуации (Ф): глубина реки с самолета измерена.

Р1 — измерение глубины реки. Но с самолета это можно сделать при помощи груза на веревке.

Ф1 — измерение с самолета.

Р2 — с самолета можно измерить какой-либо видимый горизонтальный размер, длину чего-нибудь.

Известны три стороны. Ф2 — превращение глубины реки в какой-либо видимый горизонтальный размер. Однако в этом, собственно говоря, нет ничего фантастического.

Исчислением размеров занимается тригонометрия. Если сбросить с самолета груз Р с двумя буйками, закрепленными веревками известной длины А1 и А2, то, определив с самолета расстояние между буйками а, можно найти глубину реки, как высоту треугольника, у которого известны три стороны (рис. 5.2).

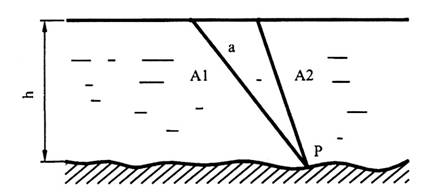
Рис. 5.2. Схема измерения глубины реки