Для изучения внутреннего строения и структуры совокупности применяются особые виды средних величин – структурные средние. К таким показателям относятся мода и медиана.

Мода (М₀) – это наиболее часто встречающаяся величина признака. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.д.

Медиана (М_е) – это такая величина признака, которая делит упорядоченный вариационный ряд на две равные части – со значениями признака меньше медианы и со значением признака больше медианы.

Расчет моды и медианы в дискретном ряду.

Пример. По имеющимся данным о выработке вычислить моду и медиану.

Таблица 5.3

1)  Наиболее часто встречающаяся выработка – 7 деталей, следовательно, М₀ = 7.

2)  Определим накопленные частоты (гр. 3 табл.5.3).

3)  Находим значение , первая накопленная частота, превышающая величину А, указывает на нахождение медианы, следовательно, М_е = 7. Итак, медианным значением выработки деталей является выработка, равная 7 деталям, т.е. половина рабочих производит до 7 деталей, а другая половина – более 7 деталей в час.

Расчет моды и медианы в интервальном ряду.

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле

,

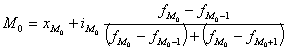где  — нижняя граница модального интервала;

 — модальный интервал;

 — частоты в модальном, предыдущем и следующем за модальным интервалом (соответственно). Модальный интервал определяется по наибольшей частоте.

В  интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле

,

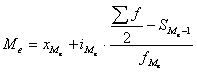где  — нижняя граница медианного интервала;

 — медианный интервал;

 — половина  от общего числа наблюдений (А);

 — сумма наблюдений, накопленная до начала медианного интервала;

 — число наблюдений в медианном интервале.

Пример. Рассчитать моду и медиану по данным табл. 5.4.

Таблица 5.4

1) Половина от общего числа наблюдений: .

2) 

Следовательно, наиболее часто встречающийся товарооборот предприятий – 104,16 тыс. р., половина предприятий имеет товарооборот до 104,58 тыс. р.,  другая половина – более 104,58 тыс. р.

Медиана находит практическое применение в маркетинговой деятельности, т.к. имеет особое свойство – сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая: .

Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда.

Мода и медиана являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.

Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части – квартили, на пять равных частей – квинтили, на десять частей – децили, на сто частей – перцентили.