Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Она является следствием действия на единицы совокупности различных факторов, которые по-разному сочетаются в каждом отдельном признаке, поэтому величина каждого варианта объективна.

Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания.

Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее.

Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию для принятия научно обоснованных управленческих решений.

Показатели вариации относят к числу обобщающих показателей, так как они измеряют вариации в совокупности явлений.

Степень колеблемости отдельных значений признака от средней отражают следующие обобщающие показатели вариации:

- размах вариации R;

- среднее линейное отклонение ;

- дисперсия  σ²;

- среднее квадратическое отклонение σ;

- коэффициент вариации V.

Значение показателей вариации заключается в следующем:

1) показатели вариации дополняют средние величины, за которыми скрываются индивидуальные различия;

2) показатели вариации характеризуют степень однородности совокупности;

3) показатели вариации характеризуют амплитуду колебания признака в совокупности;

4) соотношение показателей вариации характеризуют взаимосвязь между признаками.

Самым элементарным показателем вариации является размах вариации R, который характеризует границы вариации признаков. Он определяется как разность между максимальным и минимальным значениями признака:

.

Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. Для анализа вариации необходимы показатели, которые отражают все колебания  варьирующего признака и дают обобщенную характеристику.

Показатели такого типа:

1) Среднее линейное отклонение  — это средняя арифметическая из абсолютных отклонений, вариант от средней величины. Измеряется в двух аспектах:

для несгруппированных данных

,

где - среднее значение признака,

п – число членов ряда;

для сгруппированных данных

,

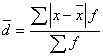где  — сумма частот вариационного ряда.

С его помощью, например, анализируется состав работающих, ритмичность производства, оборот внешней торговли.

2)  Дисперсия  — это средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

простая дисперсия для несгруппированных данных:

,

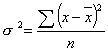взвешенная дисперсия для сгруппированных данных:

.

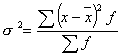3)  Среднее квадратическое отклонение  — это корень квадратный из дисперсии. Определяется также по формуле взвешенного и невзвешенного

,

для несгруппированных данных

,

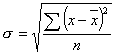для сгруппированных данных

.

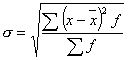В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и измеряется в единицах измерения варьирующего признака (рублях, процентах, тоннах и т.д.).

4) Коэффициент вариации V – используют для сравнения величины вариации различных признаков, а также сравнений колеблемости одного и того же признака в нескольких совокупностях. Этот показатель служит также для характеристики однородности совокупности.

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

.

Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.

Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, и тем совокупность по своему составу менее однородна.

Если совокупность разнородна, то ее нельзя использовать для производства прогнозов.

По данным о распределении рабочих по тарифному разряду рассчитать показатели вариации:

 

Тарифный разряд, хi	2	3	4	5	6
Число рабочих, fi	8	16	17	12	7

Определяем средний тарифный разряд рабочих по средней арифметической взвешенной

.

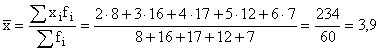Расчет основных показателей вариации оформим в таблице:

хi	fi		fi
2 3 4 5 6	8 16 17 12 7	1,9 0,9 0,1 1,1 2,1	15,2 14,4 1,7 13,2 14,7	28,88 12,96 0,17 14,52 30,87
å	60	-	59,2	87,40

а) среднее линейное отклонение ,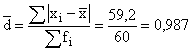

б) дисперсия ,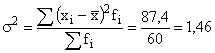

в) среднее квадратическое отклонение ,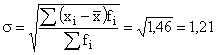

г) коэффициент вариации .