Пусть имеется игра без седловой точки с матрицей (а_ij) (табл. 5.12). Допустим, что все выигрыши а_ij положительны (этого всегда можно добиться, прибавляя ко всем членам матрицы достаточно большое число М; от этого цена игры увеличится на М, а решение , v не изменится). Если все а_ij положительны, то, конечно, и цена игры (средний выигрыш при оптимальной стратегии) тоже положительна: v > 0.

Мы хотим найти решение игры, т.е. две оптимальные смешанные стратегии:

= (р₁,  р₂, …, р_m);  = (q₁, q₂, …, q_n) ,

дающие каждой стороне максимально возможный для нее средний выигрыш (минимальный проигрыш).

Таблица 5.12 Заданная матрица игры

Найдем сначала . Мы знаем, что если один из игроков (в данном случае это А) применяет свою оптимальную стратегию, то другой (В) не может улучшить свое положение, отступая от своей оптимальной стратегии. Заставим противника (В) отступать от своей оптимальной стратегии, пользуясь чистыми стратегиями B₁, B₂,…, В_п (а мы тем временем упорно держимся стратегии ). В любом случае наш выигрыш будет не меньше, чем v:

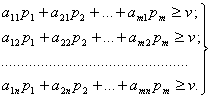                       (5.1)

Разделим неравенства (5.1) на положительную величину v и введем обозначения:

               (5.2)

Тогда условия (5.1) примут вид:

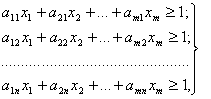                      (5.3)

где х₁, х₂, …, х_т – неотрицательные переменные.

Согласно выражению (5.2) и того, что

p₁ + р₂ + …+ p_m = 1,

переменные х₁, х₂, …, х_т удовлетворяют условию:

х₁ + х₂ + …+ х_т = 1/v.                        (5.4)

Но v есть не что иное, как наш гарантированный выигрыш; естественно, мы хотим сделать его максимальным, а значит, величину 1/v минимальной.

Таким образом, задача решения игры свелась к математической задаче: найти неотрицательные значения переменных х₁, х₂, …, х_т такие, чтобы они удовлетворяли линейным ограничениям-неравенствам (5.3) и обращали в минимум линейную функцию этих переменных:

х₁ + х₂+ …+ х_т => min.                     (5.5)

Таким образом, задача решения игры свелась к задаче линейного программирования с п ограничениями-неравенствами и т переменными. Зная х₁, х₂, …, х_т, можно найти цену игры v, а по формулам (5.2) найти p₁, р₂, …, p_m и, значит, оптимальную стратегию .

Оптимальная стратегия игрока В находится аналогично, с той разницей, что В стремится минимизировать, а не максимизировать выигрыш, а значит, обратить не в минимум, а в максимум величину 1/v, а в ограничениях-неравенствах вместо знаков ³ будут стоять знаки £. Пара задач линейного программирования, по которой находятся оптимальные стратегии (), является парой двойственных задач линейного программирования.

Таким образом, решение игры  эквивалентно решению пары задач линейного программирования. Нужно заметить, что и, наоборот,  для любой пары двойственных задач линейного программирования может быть построена эквивалентная ей матричная игра (на том, как это делается, мы останавливаться не будем).