Теорема 1

Пусть (X,£) и (Y,£) – конечные частично упорядоченные множества, m_X: X´X® Z  и   m_Y: Y´Y® Z   – их функции Мебиуса. Тогда, для любых x₁, x₂ Î X   и  y₁, y₂ Î Y имеет место равенство:

m_X´Y ( (x₁, y₁), (x_2, y₂ ) ) = m_X (x₁, x₂) m_Y (y₁, y₂).

Доказательство

Введем дзета-функцию z_X: X´X® Z, с помощью формулы:

z_X ( x₁, x₂ ) = 1 Û x₁ £ x_2.

Достаточно доказать формулу:

,

где  d_a,b – символ Кронекера.

Вычислим левую часть доказываемой формулы:

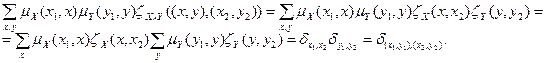
Получили, что она равна правой части. Что и требовалось доказать.

Пример 1

Вычислим  в частично упорядоченном множестве делителей числа n ≥ 1. По доказанной теореме, в случае разложения  n = в произведение степеней различных простых чисел p_i > 1, будет иметь место соотношение:

.

Поскольку

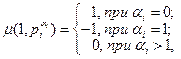
то имеем

m(1,n) = 0, если существует i такой, что a_i  > 1,

m(1,n) =(-1)^m, если n = p₁p₂ …p_{m .}

Упражнения

Диаграмма Хассе

1. Нарисовать диаграмму Хассе множества подмножеств из {0,1,2,3}, упорядоченное отношением включения.

2. Нарисовать диаграмму Хассе множества делителей числа 1000, упорядоченного отношением делимости.

3. Нарисовать диаграмму Хассе множества делителей числа 360, упорядоченного отношением делимости.

4. Нарисовать диаграмму Хассе множества P₃ разбиений множества {1,2,3}.

5. Нарисовать диаграмму Хассе множества P₄  разбиений множества {1,2,3,4}.

6. Нарисовать диаграмму Хассе произведения P₃ ´[1].

Функция Мебиуса

7. Вычислить значения m(0, x) непосредственно из определения функции Мебиуса для следующих частично упорядоченных множеств, заданных с помощью диаграмм Хассе, приведенных на рис. 5.4. 

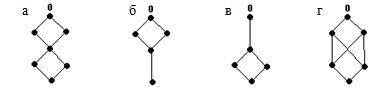
Рис. 5.4. Примеры диаграмм Хассе

1. Вычислить значения функции Мебиуса для множества P({1,2, …, n}),  упорядоченного отношением Í.

2. Пусть a – произвольный  элемент частично упорядоченного множества. Доказать, что . Найти значения функций Мебиуса для задачи 1 с помощью этой формулы.