Если винт нагружен осевой силой (F) (рис. 5.11), то для завинчивания гайки к ключу необходимо приложить момент , а к стержню винта – реактивный момент , который удерживает стержень от вращения. При этом можно записать:

, (5.2)

где  – момент сил в резьбе;  – момент сил трения на опорном торце гайки.

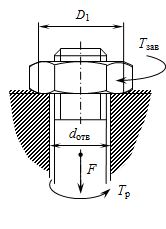
Рис. 5.11. Нагружение резьбового соединения

Приведенный радиус сил трения на опорном торце гайки с незначительной погрешностью принимают равным среднему радиусу этого торца:

,

где  – средний диаметр опорной поверхности; D₁ – наружный диаметр опорного торца гайки,  – диаметр отверстия под винт.

Тогда момент сил трения на опорном торце гайки будет определяться по формуле:

,   (5.3)

где f – коэффициент трения на опорном торце гайки.

Момент сил в резьбе определим, рассматривая гайку как ползун, поднимающийся по виткам резьбы, как по наклонной плоскости (рис. 5.12, а).

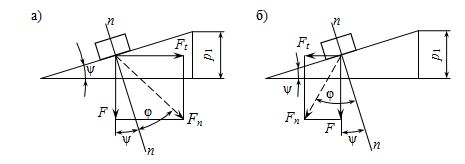
Рис. 5.12. К определению момента

По известной теореме механики, учитывающей силы трения, ползун находится в равновесии, если равнодействующая системы внешних сил () отклонена от нормали n – n на угол трения (φ). В рассматриваемом случае внешними являются осевая сила (F) и окружная сила . В данном случае  – не реактивный, а активный момент со стороны ключа, в соответствии с формулой (5.2) равный .

Окружную силу (рис. 5.12, а) определяем по формуле:

или

, (5.4)

где ψ – угол подъема резьбы, определяемый по формуле (5.1).

Угол трения в резьбе определяется по формуле:

,

где  – приведенный коэффициент трения в резьбе, учитывающий влияние угла профиля; ; f – действительный коэффициент трения.

Подставляя значения моментов, определяемые по формулам (5.3) и (5.4) в формулу (5.2), получим:

.  (5.5)

При отвинчивании гайки окружная () и нормальная () силы меняют направление (рис. 5.12, б). В данном случае будем иметь:

.

Момент отвинчивания с учетом трения на торце гайки определяется по формуле, аналогичной  формуле (5.5):

.    (5.6)