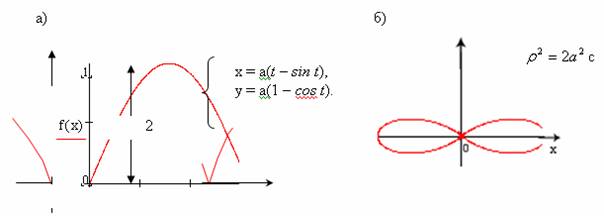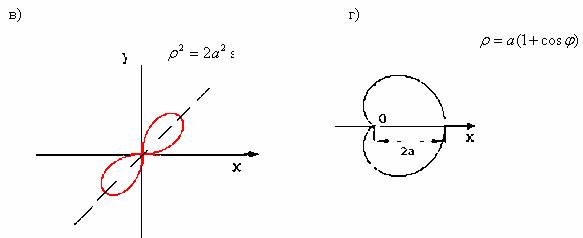При решении задач механики, сопротивления материалов, теории механизмов машин, строительства и техники, связанных с преобразованием систем координат, используют:
1) Параллельный перенос системы координат: x¢ = x - p, y¢ = y – q,
где О¢(p, q) – новое начало, (х, у) – старые координаты точки, (х¢, y¢) — новые координаты.
2) Поворот системы координат:
cos![]() ,
,
где (х, у) – старые координаты точки (при неподвижном начале), (x¢, y¢) – новые координаты, ![]() — угол поворота; причем:
— угол поворота; причем:
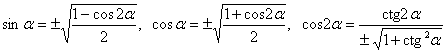 ,
,
где ![]() а общее уравнение линии второго порядка имеет вид
а общее уравнение линии второго порядка имеет вид
Ax2 + 2Bxy + Сy2 + Dx + Ey + F = 0.
Пример 1: Привести линию ![]() к каноническому виду.
к каноническому виду.
Здесь A = 2,5; 2B = -3; C = 2,5; D = -12; E = 4; F = 12.
Из ctg2![]() , тогда
, тогда ![]() и формулы поворота дают
и формулы поворота дают 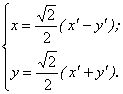
Подставив эти значения в исходное уравнение, будем иметь
![]()
Выделив полные квадраты и используя формулы параллельного переноса
![]() ,
,
придем к уравнению
![]() — эллипс с а = 2, b = 1.
— эллипс с а = 2, b = 1.
3) Расстояние между точками ![]()
![]() .
.
4) Координаты точки М(х, у), делящей отрезок ![]() , в данном отношении
, в данном отношении ![]()
![]()
при ![]() = 1 (М — середина отрезка) x = (x1 + x2) / 2, y = (y1 + y2) / 2.
= 1 (М — середина отрезка) x = (x1 + x2) / 2, y = (y1 + y2) / 2.
5) Площадь треугольника с вершинами ![]() и
и ![]()
![]()
Пример 2: Вычислить площадь листа жести, имеющего форму треугольника с вершинами M1(-2, -1), M2(3, 5) и M3(-1, 4).
Решение: Используя предыдущую формулу (знак берут таким, чтобы для площади получилось положительное число):
S = 0,5 [(3 + 2) (4 + 1) — (-1 + 2) (5 + 1)] = 9,5 (ед2).
6) Уравнение прямой с угловым коэффициентом
y = kx + b,
где ![]() — угловой коэффициент прямой к оси ОХ и b - отрезок, отсекаемый прямой на оси ОУ.
— угловой коэффициент прямой к оси ОХ и b - отрезок, отсекаемый прямой на оси ОУ.
7) Определение угла a между прямыми с угловыми коэффициентами k1 и k2:
![]() .
.
8) Условие параллельности и перпендикулярности прямых
![]()
![]() .
.
Если прямые заданы общими уравнениями
![]() и
и ![]() ,
,
то
![]() . (5.1)
. (5.1)
Пример 3: Найти угол между прямыми 10x + 6y + 30 = 0, x + 4y – 7 = 0.
Решение: По формуле (5.1): A1 = 10, B1 = 6, A2 = 1, B2 = 4, тогда
![]() .
.
Пример 4: Составить уравнение прямой, проходящей через точку М(2;-1) и параллельной прямой 3х + 4у + 10 = 0.
Решение: Искомое уравнение будет: 3х + 4у + С = 0, где С пока не определено. Используем условие А1 = ![]() А2, В1=
А2, В1=![]() В2 - условие параллельности. Подставим координаты точки М(2;-1) в искомое уравнение (ибо точка лежит на ней): 3х + 4у + С = 0, получим
В2 - условие параллельности. Подставим координаты точки М(2;-1) в искомое уравнение (ибо точка лежит на ней): 3х + 4у + С = 0, получим ![]() , откуда С = -2; таким образом, уравнение искомой прямой будет: 3х + 4у – 2 = 0.
, откуда С = -2; таким образом, уравнение искомой прямой будет: 3х + 4у – 2 = 0.
Пример 5: Составить уравнение прямой, проходящей через точку М(-5, 2) и перпендикулярной прямой 2x + 3y – 9 = 0.
Решение: Разрешив уравнение 2x + 3y – 9 = 0 относительно у, будем иметь ![]()
![]() . Видим, что k1 =
. Видим, что k1 = ![]() , тогда
, тогда ![]() . Свободный член С определим из условия, что точка М(-5, 2) лежит на искомой прямой
. Свободный член С определим из условия, что точка М(-5, 2) лежит на искомой прямой ![]() . Подставив значения x = -5, y = 2, найдем С =
. Подставив значения x = -5, y = 2, найдем С = ![]() . Искомая линия: y =
. Искомая линия: y = ![]() .
.
9) Уравнение прямой, проходящей через заданную точку ![]()
![]() .
.
10) Уравнение прямой, проходящей через две точки М1(х1, у1) и М2(х2, у2):
![]() — уравнение прямой в виде пропорций.
— уравнение прямой в виде пропорций.
11) Параметрические уравнения прямой, проходящей через две точки:
![]()
(приравняли каждое из отношений предыдущей формулы параметру t).
Пример 6: Составить параметрические уравнения прямой, проходящей через точки ![]() и
и ![]() .
.
Решение: Используя формулы, получаем:
![]() то есть
то есть ![]() .
.
12) Уравнение прямой в отрезках:
![]() ,
,
где a и b — величины направленных отрезков, отсекаемых соответственно на оси ОХ и оси ОУ.
Пример 7: Найти величины отрезков, отсекаемых на осях координат прямой, заданной уравнением 3x + 4y – 12 = 0.
Решение: Перенесем в правую часть свободный член и на него разделим полученное равенство: ![]() .
.
Сравнивая полученное уравнение с уравнением в отрезках, утверждаем, что а = 4, b = 3.
13) Общее уравнение прямой: Ах + Ву + С = 0 (А2 + В2 ![]() 0).
0).
14) Расстояние точки М0(х0, у0) от прямой Ах + Ву + С = 0:
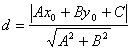 .
.
Пример 8. Определить расстояние от точки М0(-3; 2) до прямой 5х — 3у – 30 = 0.
Решение: воспользуемся формулой, получим, что
 .
.
15) Уравнение биссектрис между двумя прямыми А1х+В1х+С1=0 и А2х+В2х+С2=0:
 =
= 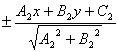 .
.
Пример 9. Составить уравнение биссектрис углов, образованных прямыми
![]()
Решение: Согласно формуле, получим
![]() .
.
Преобразовав это уравнение, найдём:
![]() ,
,
![]()
![]()
![]() ,
,
![]() — уравнения биссектрис.
— уравнения биссектрис.
16) Уравнение окружности с центром в точке О1(х1, у1) с радиусом R:
![]() .
.
Если точка О1(0; 0), то х2 + у2 = R2.
Замечание: Если уравнение второй степени не содержит члена с произведением координат ху и имеет равные коэффициенты при х2 и у2, то есть Ах2 + Ау2+Dx+Ey + F=0, тогда оно определяет окружность.
Пример 10: Найти координаты центра и радиус окружности х2 + 4х + у2 - 2у – 3 =0.
Решение: Выделим полные квадраты относительно х и у:
![]()
откуда ![]() и R =
и R = ![]() .
.
17) Каноническое уравнение эллипса с полуосями а и b:
![]() .
.
Фокусы эллипса F(с, 0) и F1(-с, 0), где с2 = а2 - b2.
Эксцентриситет: ![]() .
.
Фокальные радиусы точки М(х, у) эллипса: r =![]() .
.
Прямые ![]() — директрисы эллипса.
— директрисы эллипса.
Пример 11. Какую линию определяет уравнение ![]() ?
?
Решение: Разделив левую и правую части уравнения на 6, получим каноническое уравнение эллипса: ![]() откуда полуоси:
откуда полуоси: ![]() . Фокусы: с2 = a2 - b2, с2 = 4 – 3 = 1, с = 1. Следовательно, F1(-1, 0), F2(1, 0). Фокальные радиусы точки М(х, у):
. Фокусы: с2 = a2 - b2, с2 = 4 – 3 = 1, с = 1. Следовательно, F1(-1, 0), F2(1, 0). Фокальные радиусы точки М(х, у): ![]() и
и ![]() .
.
18) Гипербола: ![]() ; F1(-с, 0) и F2(с, 0), где с2 = а2 + b2, а — действительная и b — мнимая полуоси гиперболы.
; F1(-с, 0) и F2(с, 0), где с2 = а2 + b2, а — действительная и b — мнимая полуоси гиперболы.
Фокальные радиусы: ![]() ,
, ![]() , где
, где ![]() — эксцентриситет гиперболы.
— эксцентриситет гиперболы.
Асимптоты гиперболы: ![]() .
.
Директрисы гиперболы: ![]() .
.
Равносторонняя гипербола: ![]() .
.
19) График обратной пропорциональности ![]() — равносторонняя гипербола с асимптотами х = 0 и у = 0.
— равносторонняя гипербола с асимптотами х = 0 и у = 0.
Пример 12. Какую линию задаёт уравнение ![]() ?
?
Решение: Разделим почленно заданное уравнение на 36, получим каноническое уравнение гиперболы ![]() с действительной полуосью а = 2, мнимой полуосью b = 3. Координаты фокусов: с2 = 4 + 9 = 13, с =
с действительной полуосью а = 2, мнимой полуосью b = 3. Координаты фокусов: с2 = 4 + 9 = 13, с = ![]() ,
, ![]() и
и ![]() .
.
Эксцентриситет: ![]() ; директрисы:
; директрисы: ![]() ; асимптоты:
; асимптоты: ![]() ; фокальные радиусы, например, точки М(2;3) гиперболы:
; фокальные радиусы, например, точки М(2;3) гиперболы: ![]()
![]() ,
, ![]()
![]() . Заметим, что
. Заметим, что ![]() , т.е.
, т.е. ![]() .
.
20) Каноническое уравнение параболы с параметром р:
у2 = 2рх.
Фокус параболы: ![]() ; уравнение директрисы:
; уравнение директрисы: ![]() , фокальный радиус точки параболы:
, фокальный радиус точки параболы: ![]() .
.
Пример 13: Найти координаты фокуса и уравнение директрисы параболы y2 = 8x.
Решение: Сравнив данное уравнение с каноническим, видно, что 2p = 8, р = 4, ![]() . Директриса: x = -2, фокус параболы находится в точке F(2, 0). Фокальный радиус, например, для точки M(2, 4) будет
. Директриса: x = -2, фокус параболы находится в точке F(2, 0). Фокальный радиус, например, для точки M(2, 4) будет ![]() .
.
20) График квадратного трехчлена ![]() — парабола с вершиной
— парабола с вершиной
O1(![]() ) (вертикальная парабола).
) (вертикальная парабола).
21) Полярные координаты точки с прямоугольными координатами х и у:
![]() .
.
Прямоугольные координаты точки с полярными координатами ![]() и
и ![]() :
:
![]() .
.
22) Параметрические уравнения окружности радиуса R с центром в начале координат:
x = R cos t, y = R sin t, где t – параметр ![]() .
.
23) Параметрические уравнения эллипса с полуосями a и b: x = ac cos t, y = b sin t, ![]() .
.
24) Параметрические уравнения циклоиды (рис. 5.1, а):
![]() .
.
25) Лемниската Бернулли (рис. 5.1, б, в) в декартовых координатах имеет уравнение
![]() ;
;
в полярных ![]() .
.
26) Кардиоида: параметрические уравнения кардиоиды:
![]() ,
, ![]() :
:
- в полярных координатах (рис. 5.1, г) ![]()
- в декартовых координатах ![]() .
.
Здесь r — радиус окружности, катящейся по окружности с таким же радиусом (см. рис. 5.1).
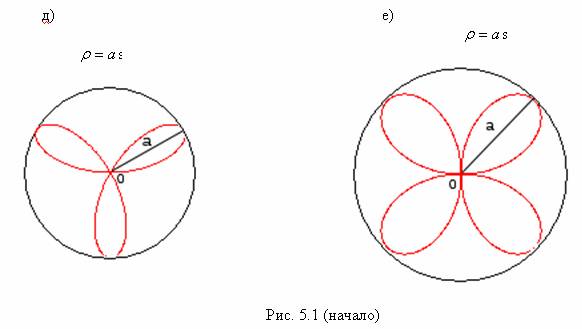
27) Розы: линии заданы уравнениями ![]() или
или ![]() , где а, к>0, если
, где а, к>0, если
![]() — четырехлепестковая роза;
— четырехлепестковая роза;
![]() — трехлепестковая роза (рис. 5.1, е, д).
— трехлепестковая роза (рис. 5.1, е, д).
28) Алгебраические спирали
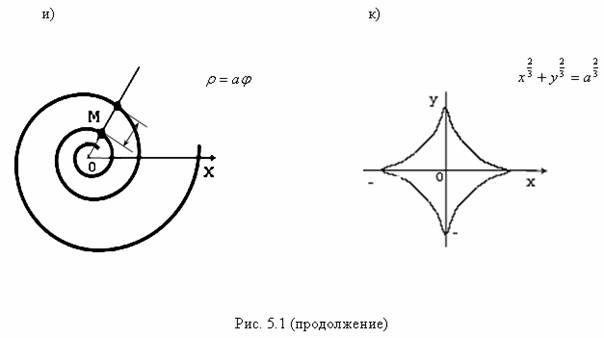
а) спираль Архимеда ![]() (рис. 5.1, и);
(рис. 5.1, и);
б) гиперболическая спираль ![]() ;
;
в) спираль Галилея ![]() ;
;
г) спираль Ферма ![]() ;
;
д) логарифмическая спираль ![]() .
.
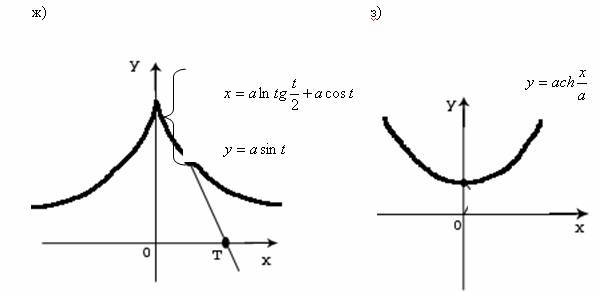
29) Трактрисса – линия, у которой длина касательной является постоянной величиной. Параметрические уравнения (рис. 5.1, ж)
![]()
Замечание: Трактрисса применяется в одной из частей механизма карусельного токарного станка.
30) Цепная линия: ![]() — кривая, форму которой принимает под действием силы тяжести нить (трос) с закрепленными концами. Уравнение цепной линии записывают и так:
— кривая, форму которой принимает под действием силы тяжести нить (трос) с закрепленными концами. Уравнение цепной линии записывают и так: ![]() где ch – гиперболический косинус (рис. 5.1, з).
где ch – гиперболический косинус (рис. 5.1, з).
31) Астроида – кривая, заданная уравнением:
![]() .
.
Параметрические уравнения астроиды: x = a cos3 t, y = a sin3 t (рис. 5.1, к).