Резервированным соединением изделий называется такое соединение, при котором отказ наступает только после отказа основного изделия и всех резервных изделий.

На практике применяются общие и раздельные способы резервирования (рис. 5.1). Общим резервированием называется метод повышения надежности, при котором резервируется изделие в целом. Раздельным резервированием называется метод повышения надежности, при котором резервируются отдельные части изделия.

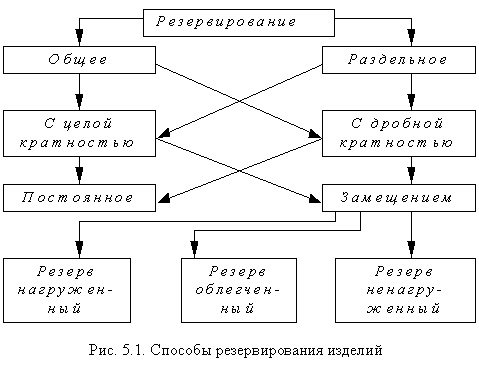Основным параметром резервирования является его кратность. Под кратностью резервирования (m) понимается отношение числа резервных изделий к числу резервируемых (основных).

Различают резервирование с целой и дробной кратностью. Схемные обозначения обоих видов резервирования при постоянном включении резерва одинаковы. Для их различия на схеме указывается кратность резервирования (m).

При резервировании с целой кратностью величина m есть целое число, при резервировании с дробной кратностью величина m есть дробное несокращаемое число.

По способу включения резервирование разделяется на постоянное и резервирование замещением. Постоянное резервирование – резервирование, при котором резервные изделия подключены к основным в течение всего времени работы и находятся в одинаковом с ними режиме. Резервирование замещением – резервирование, при котором резервные изделия замещают основные после их отказа.

При включении резерва по способу замещения резервные элементы до момента включения в работу могут находиться в трех состояниях:

· в нагруженном резерве;

· в облегченном резерве;

· в ненагруженном резерве.

Приведем основные расчетные формулы для указанных видов резервирования.

Общее резервирование с постоянно включенным резервом и с целой кратностью

Вероятность безотказной работы определяется по формуле:

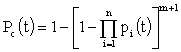,                                         (5.1)

где p_i(t) – вероятность безотказной работы i- го элемента в течение времени t; n- число элементов основной или любой резервной цепи; m – число резервных цепей (кратность резервирования).

При экспоненциальном законе надежности, когда, вероятность безотказной работы и среднее время безотказной работы определяются следующим образом:

;                                               (5.2)

,

где:  – интенсивность отказов нерезервированной системы или любой из m резервных систем; Т_{ср о} – среднее время безотказной работы нерезервированной системы или любой из m резервных систем.

При резервировании неравнонадежных изделий

,                                             (5.3)

где q_i(t), p_i(t) – вероятность отказов и вероятность безотказной работы в течение времени t_i-го изделия соответственно.

Раздельное резервирование с постоянно включенным резервом и с целой кратностью

Вероятность безотказной работы определяется по формуле:

,                                        (5.4)

где p_i(t) – вероятность безотказной работы i-го элемента; m_i – кратность резервирования i-го элемента; n – число элементов основной системы.

При экспоненциальном законе надежности, когда ,

.                                        (5.5)

При равнонадежных элементах и одинаковой кратности их резервирования

;                                           (5.6)

,                      (5.7)

где .

Общее резервирование замещением с целой кратностью

Вероятность безотказной работы определяется по формуле:

,                                      (5.8)

где Р_m+1(t), Р_m(t) – вероятности безотказной работы резервированной системы кратности m + 1 и кратности m соответственно; Р(t – t) – вероятность безотказной работы основной системы в течение времени (t – t); a_m(t) – частота отказов резервированной системы кратности m в момент времени t.

Рекуррентная формула (3.8) позволяет получить расчетные соотношения для устройств любой кратности резервирования. Для получения таких формул необходимо выполнить интегрирование в правой части, подставив вместо  Р(t – t) и а_m(t) их значения в соответствии с выбранным законом распределения и состоянием резерва.

При экспоненциальном законе надежности и ненагруженном состоянии резерва

;                                             (5.9)

,                                              (5.10)

где l₀, Т_{ср о} – интенсивность отказов и средняя наработка до первого отказа основного (нерезервированного) устройства.

При экспоненциальном законе и недогруженном состоянии резерва

                                  (5.11)

                                                 (5.12)

где  l₁ – интенсивность отказов резервного устройства до замещения.

При нагруженном состоянии резерва формулы для Р_с (t) и T_{cp c} совпадают с формулами (5.2).

Раздельное резервирование замещением с целой кратностью

Вероятность безотказной работы определяется по формуле:

,                                                 (5.13)

где р_i(t) – вероятность безотказной работы системы из-за отказов элементов i-го типа, резервированных по способу замещения. Вычисляется Р_i(t) по формулам общего резервирования замещением (5.8), (5.9), (5.11).

Общее резервирование с дробной кратностью и постоянно включенным резервом

Вероятность безотказной работы и среднее время безотказной работы определяются по формулам:

;                                   (5.14)

,                                                (5.15)

где p₀(t) – вероятность безотказной работы основного или любого резервного элемента; l – общее число основных и резервных систем; h – число систем, необходимых для нормальной работы резервированной системы.

В данном случае кратность резервирования равна:

.                                                      (5.16)

Скользящее резервирование

Вероятность безотказной работы определяется по формуле:

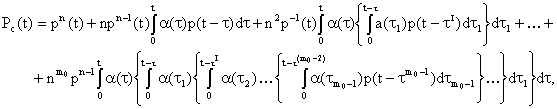
 (5.17)

где   ; n – число элементов основной системы; m₀ – число резервных элементов; p(t – t _i) – вероятность безотказной работы одного элемента в течение времени t – t _I (t_i = t, t – t, …); α(t_i) – частота отказов одного из основных элементов в момент времени t_I ().

При экспоненциальном законе надежности

;   (5.18)

где l₀ = nl – интенсивность отказов нерезервированной системы; l – интенсивность отказов элемента; n – число элементов основной системы; Т_{ср о –} среднее время безотказной работы нерезервированной системы; m₀ – число резервных элементов.

В этом случае кратность резервирования

.                                                     (5.19)

Все формулы, приведенные в этом разделе, кроме выражений (5.8), (5.11), (5.12), могут быть использованы только в тех случаях, когда справедливо допущение об отсутствии последствия отказов. Последствие отказов имеются практически всегда при постоянном включении резерва, а также в случае резервирования замещением при недогруженном состоянии резерва.

Выражение (5.8) является основным при получении расчетных формул в случае учета влияния последствия отказов. При этом члены p(t – t) и α_m(t) должны быть записаны с учетом последствия отказов, вида резервирования и его кратности.

Элементы резервированных устройств в ряде случаев могут иметь два вида отказов: «обрыв» и «короткое замыкание». В этом случае вычислять вероятность безотказной работы следует, суммируя вероятности всех благоприятных (не приводящих к отказу) гипотез, т.е.

,                                                 (5.20)

где р_j(t) – вероятность j-й благоприятной гипотезы, вычисленной с учетом двух видов отказов; k – число благоприятных гипотез.

При вычислениях p_j(t) следует иметь в виду, что для элементов сложной системы справедливы выражения:

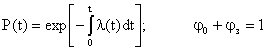,                                  (5.21)

где l(t) – интенсивность отказов элемента; j₀, j_з – вероятность возникновения «обрыва» и «короткого замыкания» соответственно.

При экспоненциальном законе надежности

                       (5.22)

где l₀, l_З – интенсивность отказов элемента по «обрыву» и «короткому замыканию» соответственно.

Остальные количественные характеристики надежности в случае необходимости вычисляются через Р_с(t) по известным аналитическим зависимостям.

Расчет надежности резервированных систем иногда полезно выполнять, используя схему «гибели» («чистого размножения»). В соответствии с этой схемой преобразование Лапласа вероятности возникновения n отказов вычисляется по формуле:

.                                        (5.23)

При неравных корнях знаменателя обратное преобразование Лапласа P_n(s) будет:

                                                        (5.24)

В формулах (5.23) и (5.24) приняты обозначения: l₀ – интенсивность отказов системы до выхода из строя первого элемента; l₁ – интенсивность отказов системы в промежутке времени от момента отказа первого элемента до второго; l₂ – интенсивность отказов системы в промежутке времени от момента отказа второго элемента до третьего и т.д.; n – число отказавших элементов; s_k (равный -l_k) – k-й корень знаменателя выражения (5.23); В^/(s_k) – производная знаменателя в точке s_k.

При одинаковых опасностях отказов l_i, т.е. l₀ = l₁ = ¼= l_n, расчетные формулы имеют вид:

.                           (5.25)

При расчетах надежности по формулам (5.23) – (5.25) следует помнить, что они не определяют вероятности безотказной работы (или вероятности отказа) резервированной системы, а определяют лишь вероятность n-го состояния системы, т.е. вероятность того, что в системе откажут n элементов. Для вычисления вероятности безотказной работы необходимо находить вероятности 0, 1,¼, n отказов, когда система еще находится в работоспособном состоянии (исправна), и суммировать полученные вероятности.

Среднее время безотказной работы системы при использовании схемы «гибель» вычисляется по формуле:

                                                    (5.26)

где l_i – интенсивность отказов системы до выхода из строя i-го элемента.

При схемной реализации резервирования в ряде случаев конкретные технические решения не приводят к логическим схемам расчета надежности.

В этих случаях, чтобы получить аналитические выражения для количественных характеристик надежности, следует использовать метод перебора благоприятных гипотез. Вероятность безотказной работы в этом случае вычисляется по выражению (5.20).

При анализе надежности резервированных устройств на этапе проектирования приходится сравнивать различные схемные решения. В этом случае за критерий качества резервирования принимается выигрыш надежности. Выигрышем надежности называется отношение количественной характеристики надежности резервированного устройства к той же количественной характеристике нерезервированного устройства или устройства с другим видом резервирования.

Наиболее часто используются следующие критерии качества резервированных устройств:

· выигрыш надежности в течение времени t по вероятности отказов G_q(t);

· выигрыш надежности в течение времени t по вероятности безотказной работы G_p(t);

· выигрыш надежности по среднему времени безотказной работы G_T.

При резервировании элементов электроники (резисторов, конденсаторов, контактов реле, диодов и т.п.) всегда произведение интенсивности отказов элемента на время его работы значительно меньше единицы, т.е. l(t) << 1. Поэтому при вычислении G_q(t) и G_p(t) целесообразно функции вида  (экспоненциальный случай) разложить в ряд (при небольшом k):

.

Если система исправна при отказе m элементов, то необходимо брать не менее чем m + 2 членов разложения.