Пусть на отрезке  задана сетка , в узлах которых заданы значения , где . Требуется найти число  такое, что

.

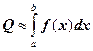Отметим, что задача численного интегрирования является корректно поставленной. Возможны два случая:

1) формула функции  задана, и по этой формуле находятся ;

2) формула функции  не задана, известна только интерполяционная таблица.

Как известно, число 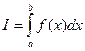    для положительных  равно площади криволинейной трапеции, ограниченной кривой , осью абсцисс и прямыми:  и  (рис. 6.1).

Основная идея численного интегрирования заключается в следующем: вместо площади криволинейной трапеции I будем считать площадь другой фигуры Q, причем должны выполняться два условия:

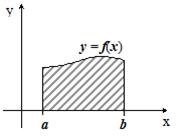
Рис. 6.1. Геометрический смысл определённого интеграла

1) площадь новой фигуры Q должна быть близка к площади криволинейной трапеции;

2) площадь новой фигуры Q должна вычисляться достаточно просто.

Площадь каких геометрических фигур вычисляется очень легко? Площадь прямоугольника  и площадь трапеции. Но, если отрезок  достаточно большой, то площадь прямоугольника или площадь трапеции будут плохо приближать площадь исходной криволинейной трапеции. Чтобы избежать этого, представим  интеграл I в виде суммы:

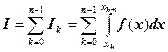
и будем приближать каждый интеграл 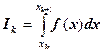  числом  , а интеграл I числом .

Таким образом, исходная криволинейная трапеция разбивается на n криволинейных трапеций, а вместо площади каждой «маленькой» криволинейной трапеции считается площадь простой фигуры, например, площадь прямоугольника или трапеции.

Рекомендуемая литература: /1-7, 14- 16/.