В классической механике справедлив механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчета.
 Связь между координатами произвольной точки
Связь между координатами произвольной точки ![]() в обеих инерциальных системах отсчета
в обеих инерциальных системах отсчета ![]() и
и ![]() , где система
, где система ![]() неподвижна, а система
неподвижна, а система ![]() движется равномерно и прямолинейно со скоростью
движется равномерно и прямолинейно со скоростью ![]() относительно системы
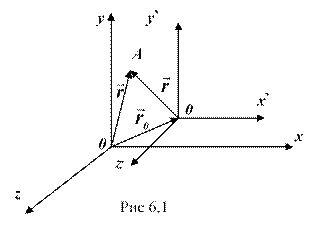
относительно системы ![]() , имеет вид (рис. 6.1.)
, имеет вид (рис. 6.1.)
![]() (6.1)
(6.1)
Уравнение (6.1) можно записать в проекциях на оси координат:
![]() ;
;
![]() ; 6.2)
; 6.2)
![]() .
.
Уравнения (6.1) и (6.2) носят название преобразования координат Галилея. В частном случае, когда система ![]() движется со скоростью
движется со скоростью ![]() вдоль положительного направления оси х системы
вдоль положительного направления оси х системы ![]() , преобразования Галилея имеют вид:
, преобразования Галилея имеют вид:
![]() .
.
В классической механике предполагается, что ход времени не зависит от относительного движения системы отсчета, то есть ![]() .
.
Продифференцировав выражение (6.1) по времени, получим:
![]() .
.
Ускорение ![]() , то есть
, то есть
![]() (6.3)
(6.3)
Таким образом, ускорения точки ![]() в системах
в системах ![]() и
и ![]() одинаковы. Из соотношения (6.3) вытекает подтверждения механического принципа относительности: уравнения динамики при переходе из одной инерциальной системы отсчета к другой не изменяются, то есть являются инвариантными по отношению к преобразованиям координат.
одинаковы. Из соотношения (6.3) вытекает подтверждения механического принципа относительности: уравнения динамики при переходе из одной инерциальной системы отсчета к другой не изменяются, то есть являются инвариантными по отношению к преобразованиям координат.