Уравнение логарифмической спирали в полярных координатах имеет следующий вид:

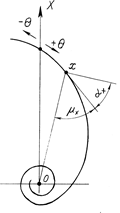
Рис. 6.19. Логарифмическая спираль

,                                                                                                                   (6.1)

где  — радиус-вектор, проведенный из начала координат в точку на кривой;  и  — постоянные коэффициенты;  — основание натуральных логарифмов;  — текущий полярный угол для данной точки кривой, в радианах.

При перемещении радиуса вектора  по часовой стрелке от полярной оси угол  положителен, против часовой – отрицателен. При =0 . Для точки «х» на кривой уравнение спирали:

.

Из дифференциальной геометрии известно, что угол  между радиусом-вектором и касательной для одной и той же точки плоской кривой определятся по формуле:

,

где  — производная уравнения кривой по параметру.

Тогда для точки  логарифмической спирали имеем:

или

.                                                                                          (6.2)

Таким образом, логарифмическая спираль, обеспечивающая постоянство заднего угла, является приемлемой кривой для затылования.

Затылованный зуб можно рассматривать состоящим из целого ряда кривых, уже не являющихся логарифмическими спиралями. Допустим, что через верхнюю часть зуба, т.е. через А и В (рис. 6.20) проходит расчетная логарифмическая спираль. Она стремится к центру фрезы, являющейся асимптотической точкой для спирали. Если через другую точку профиля С, расположенную на величину h ниже точки А, провести логарифмическую спираль, то она тоже будет стремиться к центру фрезы. Тогда расстояния  между спиралями будут все время уменьшаться: .

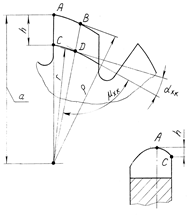
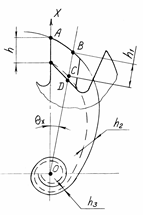
Рис. 6.20. Конхоида  логарифмической             Рис. 6.21. Задний угол на конхоиде

                    спирали                                          логарифмической спирали

Однако на практике это не имеет места, так как при затыловании высота профиля зуба h остается постоянной, что достигается постоянством формы затыловочного резца. Поэтому реально получается, что точная логарифмическая спираль проходит через одну или несколько точек профиля, а через другие точки профиля, лежащие ниже или выше расчетной, проходят другие кривые, называемые конхоидами (конхоиду можно построить по точкам, откладывая величину h от кривой АВ, рис. 6.21).

При конструировании фрезы необходимо знать величину затылования К, отнесенную к началу следующего зуба (рис. 6.22). Для определения величины К разделим центральный угол , соответствующий угловому шагу, пополам.

Тогда

,                                                                                                                     (6.3)

где z – число зубьев;

или

.                                                                                                                         (6.4)

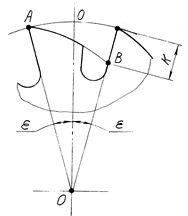
Рис. 6.22. Величина затылования

Величина затылования

.                                                                                                              (6.5)