Уравнение спирали Архимеда в полярных координатах (рис.6.23) имеет вид:

,                                                                                                                     (6.6)

где  – радиус-вектор точки на кривой;  — текущий полярный угол в радианах для точки на кривой;  — постоянный коэффициент, равный полярной поднормали; ; ; .

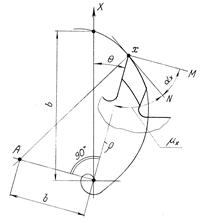
Рис. 6.23. Спираль Архимеда

Так как , а радиус-вектор есть переменная величина, то задний угол при переточках фрезы не является постоянным, а изменяется пропорционально полярному углу .

Рассмотрим изменение заднего угла в любой точке профиля (рис. 6.24). Из уравнения спирали Архимеда видно, что приращение радиуса-вектора пропорционально приращению полярного угла. Поэтому вся поверхность зуба фрезы состоит из отрезков одной и той же спирали Архимеда, являющихся ее конхоидами.

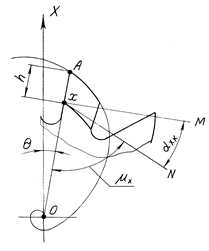
Рис. 6.24. Задний угол на конхоиде спирали Архимеда

Найдем величину затылования (рис. 6.25):

.

Для точки 1 (см.рис.6.25) уравнение спирали Архимеда . Для точки 2: .

Величина затылования или .                (6.7)

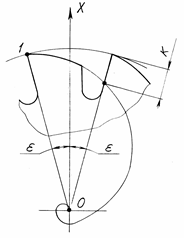
Рис. 6.25. Величина затылования