Одной из основных задач корреляционного анализа является определение влияния факторов на величину результативного показателя (в абсолютном измерении). Для решения этой задачи подбирается соответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи. Обоснование уравнения связи делается с помощью сопоставления параллельных рядов, группировки данных и линейных графиков. Размещение точек на графике покажет, какая зависимость образовалась между изучаемыми показателями – прямолинейная или криволинейная.
Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой:
Yx = a + b * х, (6.1)
где Yx – результативный показатель; а и b – параметры уравнения регрессии; x – факторный показатель.
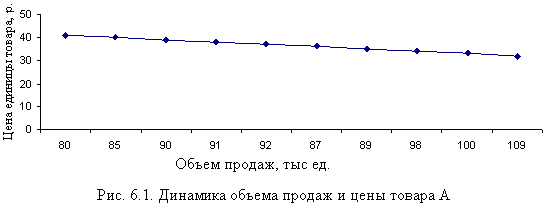
Таблица 6.1 Динамика объема продаж и цены товара А
|
Порядковый номер наблюдения |
Объем продаж, тыс. ед. |
Цена единицы товара, р. |
|
1 |
80 |
41 |
|
2 |
85 |
40 |
|
3 |
90 |
39 |
|
4 |
91 |
38 |
|
5 |
92 |
37 |
|
6 |
87 |
36 |
|
7 |
89 |
35 |
|
8 |
98 |
34 |
|
9 |
100 |
33 |
|
10 |
109 |
32 |
Это уравнение описывает такую связь между двумя признаками, при которой с изменением на определенную величину факторного показателя наблюдается равномерное возрастание или убывание значений результативного показателя. Значения коэффициентов а и b находят по следующим формулам:
![]() ; (6.2)
; (6.2)
![]() , (6.3)
, (6.3)
где n – количество наблюдений.
Рассмотрим пример (табл. 6.1). Между объемом продаж и ценой существует зависимость (рис. 6.1)
 |
Чтобы рассчитать коэффициенты а и b уравнения (6.1), составим вспомогательную таблицу 6.2.
Подставим в уравнения (6.1) и (6.2) значения величин из табл. 6.2, получим:
Таблица 6.2.
|
x |
y |
x*y |
x2 |
|
41 |
80 |
3280 |
1681 |
|
40 |
85 |
3400 |
1600 |
|
39 |
90 |
3510 |
1521 |
|
38 |
91 |
3458 |
1444 |
|
37 |
92 |
3404 |
1369 |
|
36 |
87 |
3132 |
1296 |
|
35 |
89 |
3115 |
1225 |
|
34 |
98 |
3332 |
1156 |
|
33 |
100 |
3300 |
1089 |
|
32 |
109 |
3488 |
1024 |
|
Итого 365 |
921 |
33419 |
13405 |
Промежуточные расчёты
![]() ;
;
![]() .
.
Тогда, уравнение зависимости объема продаж от цены будет иметь следующий вид:
Y = 179,481 – 2,394 * x.
Коэффициент а – постоянная независимая величина. Параметр b показывает среднее изменение результативного показателя с повышением или понижением величины факторного показателя на единицу его измерения. В данном примере с увеличением цены на 1 рубль объем реализации будет снижаться на 2,394 ед.
Для измерения тесноты связи между факторными и результативными показателями исчисляется коэффициент корреляции. В случае прямолинейной формы связи между изучаемыми показателями он рассчитывается по следующей формуле:
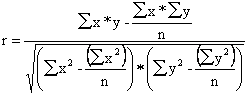 .
.
Подставив в эту формулу значения величин из табл. 6.2, получим значение коэффициента корреляции:
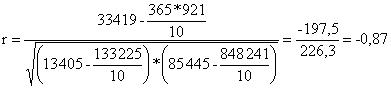 .
.
Коэффициент корреляции может принимать значения от 0 до ![]() 1. Чем ближе его значение к 1, тем более тесная связь между изучаемыми явлениями, и наоборот. В данном случае значение коэффициента корреляции стремится к единице (r = -0,87). Это позволяет сделать вывод о том, что цена товара – один из основных факторов, от которого зависит объем продаж товара А.
1. Чем ближе его значение к 1, тем более тесная связь между изучаемыми явлениями, и наоборот. В данном случае значение коэффициента корреляции стремится к единице (r = -0,87). Это позволяет сделать вывод о том, что цена товара – один из основных факторов, от которого зависит объем продаж товара А.
Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации (d = 0,757). Он показывает, что объем продаж на 75,7 % зависит цены товара, а на долю других факторов приходится 24,3 % ее прироста.
В заключение необходимо отметить, что эта методика может быть использована для исследования соотношений между разными экономическими показателями, что позволяет значительно углубить знания об изучаемых явлениях, оценить место и роль каждого фактора в изменении уровня исследуемого показателя.