Рассмотрим подробнее реализацию вычислительным устройством П-, ПИ- и ПИД-законов управления.

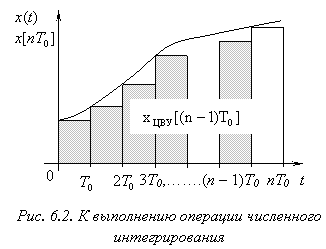Очевидно, что пропорциональное управление сводится к простому умножению дискрет  на некоторую константу , т.е.

.            (6.1)

Численное интегрирование может быть выполнено различными способами. Выбор способа определяется тем, какой из методов дискретизации интеграла от функции  реализует ЦВУ. В качестве приближенного значения интеграла можно взять площадь, ограниченную ступенчатой кривой, проведенной через дискреты интегрируемой функции     (рис. 6.2). При этом алгоритм работы на ЦВУ описывается разностным уравнением:

Применив операцию Z-преобразования к этому уравнению, получим:

,

откуда:

                                      (6.2)

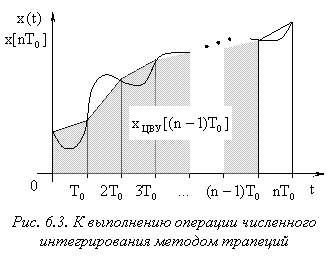
Иную передаточную функцию цифрового интегратора получим, если интегрирование производится по несколько более точному методу трапеции (рис. 6.3), согласно которому:

Выполнив Z-преобразование, получим:

тогда 

                                       (6.3)

Если более точное интегрирование можно обеспечить, применяя параболическую аппроксимацию функции . Тогда согласно формуле Симпсона реализуется следующий алгоритм:

При этом передаточная функция интегратора:

       (6.4)

Необходимо учитывать, что стремление к повышению точности интегрирования за счет повышения порядка  может привести к усложнению аппаратной реализации вычислительного устройства, а также к увеличению интервала квантования, что особенно критично для систем; управление которыми осуществляется в реальном масштабе времени.

В качестве приближенного значения производной функции  можно использовать отношение первой обратной разности решетчатой функции  к интервалу дискретности. В этом случае уравнение ЦВУ имеет вид:

а передаточная функция цифрового дифференцирующего устройства:

                                             (6.5)

Используя выражения (6.2) – (6.5), можно записать передаточные функции вычислительных устройств, реализующих более сложные законы управления. Так, передаточная функция ПИ-регулятора для случая, когда интегрирование производится по методу трапеции, равна:

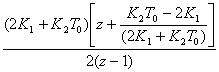=,                                       (6.6)

а передаточная функция ЦВУ, осуществляющего ПИД-закон регулирования, имеет следующий вид:

= .                    (6.7)