Пусть дана некоторая сложная целевая функция, зависящая от нескольких переменных, и требуется решить задачу оптимизации, т. е. найти такие значения переменных, при которых значение функции максимально или минимально.

Эту задачу можно решить, применяя известные биологические эволюционные подходы к оптимизации. Будем рассматривать каждый вариант (набор значения переменных) как особь, а значение целевой функции для этого варианта – как приспособленность данной особи. Тогда в процессе эволюции приспособленность особей будет возрастать, а значит, будут появляться все более и более оптимальные варианты. Остановив эволюцию в некоторый момент и выбрав лучший вариант, можно получить достаточно хорошее решение задачи.

Генетический алгоритм (ГА) – это последовательность управляющих действий и операций, моделирующая эволюционные процессы на основе аналогов механизмов генетического наследования и естественного отбора. При этом сохраняется биологическая терминология в упрощенном виде.

Хромосома – вектор (последовательность) из нулей и единиц, каждая позиция (бит) которого называется геном.

Особь (индивидуум) = генетический код – набор хромосом = вариант решения задачи.

Кроссовер – операция, при которой две хромосомы обмениваются своими частями.

Мутация – случайное изменение одной или нескольких позиций в хромосоме.

Генетические алгоритмы представляют собой, скорее, подход, чем единые алгоритмы. Они требуют содержательного наполнения для решения каждой конкретной задачи.

На рис. 6.1 показан один из вариантов структуры генетического алгоритма. Вначале генерируется случайная популяция – несколько особей со случайным набором хромосом (числовых векторов). Генетический алгоритм имитирует эволюцию этой популяции как циклический процесс скрещивания особей, мутации и смены поколений (отбора).

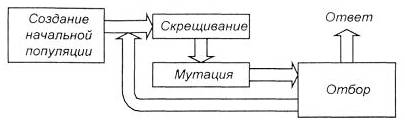
Рис. 6.1. Вариант структуры генетического алгоритма

В течение жизненного цикла популяции, т. е. в результате нескольких случайных скрещиваний (посредством кроссовера) и мутаций, к ней добавляется какое-то количество новых вариантов. Далее происходит отбор, в результате которого из старой популяции формируется новая, после чего старая популяция погибает. После отбора к новой популяции опять применяются операции кроссовера и мутации, затем опять происходит отбор, и так далее.

Отбор в генетическом алгоритме тесно связан с принципами естественного отбора следующим образом:

·  приспособленность особи соответствует значению целевой функции на заданном варианте;

· выживание наиболее приспособленных особей соответствует тому, что популяция следующего поколения вариантов формируется с учетом целевой функции. Чем приспособленнее особь, тем больше вероятность ее участия в кроссовере, т. е. в размножении.

Таким образом, модель отбора определяет, как следует строить популяцию следующего поколения. Как правило, вероятность участия особи в скрещивании берется пропорциональной ее приспособленности. Часто используется так называемая стратегия элитизма, при которой несколько лучших особей переходят в следующее поколение без изменений, не участвуя в кроссовере и отборе. В любом случае каждое следующее поколение будет в среднем лучше предыдущего. Когда приспособленность особей перестает заметно увеличиваться, процесс останавливают и в качестве решения задачи оптимизации берут наилучший из найденных вариантов.

Математически изложенное можно представить следующим образом. Пусть имеется некоторая целевая функция от многих переменных, у которой необходимо найти глобальный максимум или минимум:

Представим независимые переменные в виде хромосом. Для этого выполним кодирование независимых переменных либо в двоичном формате, либо в формате с плавающей запятой.

В случае двоичного кодирования используется  бит для каждого параметра, причем  может быть различным. Если параметр может изменяться между минимальным (min) и максимальным (max) значениями, можно использовать следующие формулы для преобразования:

где  – значение параметра в формате с плавающей запятой; – значение параметра в двоичном формате.

Хромосомы в формате с плавающей запятой задаются путем последовательного размещения закодированных параметров друг за другом.

Наиболее хорошие результаты дает вариант представления хромосом в двоичном формате (особенно, при использовании кодов Грея). Однако в этом случае необходимо постоянно осуществлять кодирование/декодирование параметров (генов).

Рассмотрим работу генетического алгоритма более подробно. Заранее подбирается некоторое представление для рассматриваемого решения, размер и структура популяции. В первом поколении случайным образом генерируется популяция хромосом. Обычно, размер популяции постоянен. Определяется «полезность» хромосом. После чего генетический алгоритм может начинать генерировать новую популяцию.

Далее осуществляется репродуцирование, состоящее:

·  из селекции;

·  трех генетических операторов: кроссовера, мутации и инверсии, порядок применения которых не важен.

Из трех генетических операторов кроссовер является наиболее важным. Он генерирует новую хромосому потомка, объединяя генетический материал двух родителей. Существует несколько вариантов кроссовера. Наиболее простым является одноточечный, в котором берутся две хромосомы и «перерезаются» в случайно выбранной точке. Хромосома потомка получается из начала одной и конца другой родительских хромосом:

001100010|11000                    ®                    00110001011100

111101000|11100

Мутация представляет собой случайное изменение хромосомы (обычно простым изменением состояния одного из битов на противоположное). Данный оператор позволяет, во-первых, более быстро находить локальные экстремумы и, во-вторых, перескочить в другой локальный экстремум:

00110000                     ®                    00110001111000

Инверсия изменяет порядок бит в хромосоме путем циклической перестановки (случайное количество раз). Многие модификации ГА обходятся без данного генетического оператора:

00110001011000                     ®                    11000001100010

По скорости определения оптимума целевой функции генетические алгоритмы на несколько порядков превосходят случайный поиск. Причина этого заключается в том, что большинство систем имеют довольно независимые подсистемы, вследствие чего при обмене генетическим материалом от каждого из родителей берутся гены, соответствующие наиболее удачному варианту определенной подсистемы (неудачные варианты постепенно погибают). Генетический алгоритм позволяет накапливать удачные решения для таких систем в целом.

Генетические алгоритмы менее применимы для систем, которые сложно разбить на подсистемы. Кроме того, они могут давать сбои из-за неудачного порядка расположения генов (например, если рядом расположены параметры, относящиеся к различным подсистемам), при котором преимущества обмена генетическим материалом сводятся к нулю. Это замечание несколько сглаживается в системах с диплоидным (двойным) генетическим набором.

Данные, которые закодированы в генотипе, могут представлять собой команды какой-либо виртуальной машины. В таком случае можно говорить об эволюционном или генетическом программировании. В простейшем случае можно ничего не менять в генетическом алгоритме. Однако в таком случае длина получаемой последовательности действий (программы) получается не отличающейся от той (или тех), которая является «затравкой» на этапе инициализации. Современные алгоритмы генетического программирования функционируют в системах с переменной длиной генотипа.