Эйнштейн показал, что в теории относительности классические преобразования Галилея, описывающие переход от одной инерциальной системы к другой:

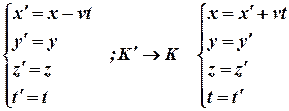
где  – покоящаяся система, - система движущаяся относительно системы  со скоростью   вдоль положительного направления оси , заменяются преобразованиями Лоренца, удовлетворяющими постулатам Эйнштейна .

Преобразования Лоренца имеют вид:

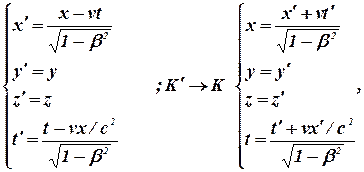
где .

Из преобразований Лоренца вытекает, что при малых скоростях, то есть когда , они переходят в классические преобразования Галилея. При  выражения   (6.1) для  и  теряют физический смысл (становятся мнимыми). Кроме того, следует, что пространственные и временные преобразования не являются независимыми, поскольку в закон преобразования координат входит время, а в закон преобразования времени – пространственные координаты, то есть устанавливается взаимосвязь пространства и времени. Неразрывно связанные пространственные и временные координаты образуют четырехмерное пространство – время.