В задачах, которые решают интеллектуальные си­стемы, иногда приходится применять ненадежные знания и факты, представить которые двумя значения­ми — истина или ложь (1 или 0) — трудно. Суще­ствуют знания, достоверность которых, скажем, 0,7. Такую ненадежность в современной физике и технике представляют вероятностью, подчиняющейся законам Байеса (для удобства назовем ее байесовской вероят­ностью), но в инженерии знаний было бы нелогично иметь дело со степенью надежности, приписанной знаниям изначально, как с байесовской вероятностью, (нелогично незнание представлять байесовской веро­ятностью).

Поэтому одним из первых был разработан метод использования коэффициентов уверенности. Этот метод не имеет теоретического подкрепления, но стал примером обработки ненадежных знаний, что оказало заметное влияние на последующие системы. Позже была введена теория вероятностей Демпстера — Шафера, которая имеет все признаки математической теории. По сравнению с байесовской вероятностью теория Демпстера — Шафера отличается тем, что она не фиксирует значения вероятности, а может представлять  и незнание.

Связь между подзадачами, на которые разбита задача, оперирующая двумя понятиями — истина и ложь, может быть представлена через операции И и ИЛИ. В задачах с ненадежными исходными данными кроме И и ИЛИ важную роль играет комбинированная связь, которую будем обозначать как КОМБ. Такая связь независимо подкрепляет или опровергает цель на основании двух и более доказательств. Ниже будет рассмотрен метод выводов в задачах, представленных таким образом. Нечеткая логика, ведущая свое происхождение от теории нечетких множеств, — это разновидность непрерывной логики, в которой логические формулы оперируют со значениями между 0 и 1. Упомянутые выше методы, продолжающие развитие теории вероятности, несколько отличаются от нечеткой логики, более субъективны, но по своей логической сущности более сильны. Вообще говоря, логика играет важную роль при рассмотрении фундаментальных понятий представления знаний и выводов. Даже принципы обработки ненадежных зна­ний основаны на логике.

Разбиение задач с ненадежными данными

Для решения сложных задач можно использовать метод разбиения их на несколько подзадач. Каждая подзадача в свою очередь разбивается на простые подзадачи, поэтому задача в целом описывается иерархически. Знания, которые по условиям подзадач определяют условия задач высшего уровня, накапли­ваются фрагментарно. В задачах с ненадежными дан­ными знания могут не только иметь степень надеж­ности, равную 1, но и промежуточные значения между истиной и ложью. Как отмечено выше, при разбие­нии на подзадачи возможно соединение И, ИЛИ и КОМБ (комбинированная связь). На рис. 6.7 пока­зано описание задачи в виде дерева И, ИЛИ, КОМБ (в общем случае это может быть граф).

На основании двух и более доказательств цели (или подцели) независимо подтверждаются или опро­вергаются (в случае противоречивых доказательств), если связь

комбинированная. Например, рассмотрим случай определения (диагностирования), простужен ли больной. Пусть доказательство 1 — кашель у боль­ного — надежно со степенью 0,6, а доказательство 2 — температура 39 — 40° — надежно со степенью только 0,5. Простудное состояние при наблюдении лишь одного из доказательств простуды можно подтвердить только с надежностью 0,6 или 0,5.

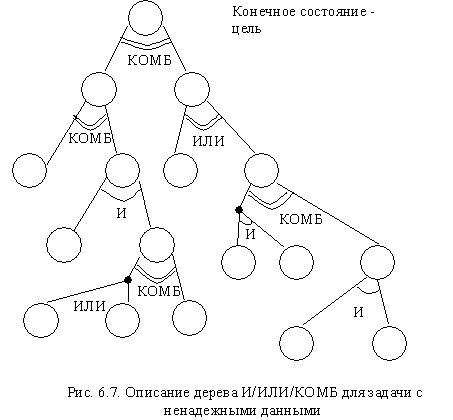
Но если рассмо­треть оба доказательства, то, естественно, нужно счи­тать, что простуда куда более достоверна. Если выполнить операцию КОМБ, то мы должны получить, скажем, надежность 0,8. И наоборот, пусть доказа­тельство 1 — наличие кашля — снова имеет надеж­ность 0,6, но температура, как доказательство 2, нор­мальная, тогда при операции комбинированной связи надежность диагноза простуды уменьшится и будет равна, например, 0,45.

Методы представления знаний, конечно, не одно­значны, но метод выводов, приведенный здесь, краток и ясен, поэтому знания будем описывать на основе представления знаний с помощью правил так, как в системе продукций. Способ записи правил, включаю­щих также и комбинированную связь, можно выбрать любой, но сейчас продолжим обсуждение, используя запись правил, указанную на рис. 6.8, где X, Y — ре­зультаты доказательств, А — цель или гипотеза, а И, ИЛИ и КОМБ - виды связей. C₁, C₂, С₃₁, С₃₂ - это степени надежности, приписанные правилам (зна­ниям).

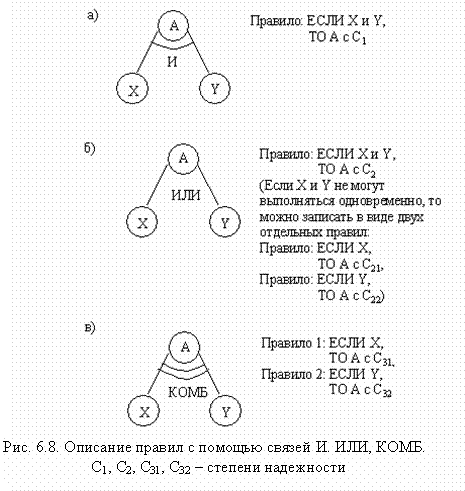Допустим, что для нашей задачи уже определены степени надежности Х и Y как результатов предыду­щих выводов или наблюдений, и сделаем вывод или вычислим степень надежности А, используя правила из базы знаний.

Кроме общеизвестных методов выбо­ра минимального значения степеней надежности из нескольких выводов при связи И и максимального при связи ИЛИ других подходящих методов не суще­ствует, а при связи КОМБ предложены рассмотренные ниже субъективный байесовский метод, а также теория Демпстера — Шафера.

Если выбрать метод выводов как для связи И, ИЛИ, так и для связи КОМБ, то степени надежности можно распространить и на иерархическую сеть вы­водов. В итоге можно получить степень надежности конечной цели, а также указать ее при окончательном ответе.

Субъективный байесовский метод

Дуда, Харт и Нильсон видоизменили формулы Байеса для выводов в инженерии знаний и предло­жили метод выводов, названный субъективным бай­есовским методом. При этом методе связи И, ИЛИ, как на рис. 6.8, а, б, специально не оговариваются, а каждый член в предпосылке представляется мини­мальным или максимальным значением байесовской вероятности. После этого выводы с помощью правил, которые содержат степени надежности, и выводы в случае связи КОМБ независимых доказательств, как на рис. 6.8, в, делаются следующим образом.

Прежде всего, из формул Байеса следуют соотношения

                

откуда

(здесь  — дополнение множества А). Кроме того если Х и Y взаимно независимые относительно А, то справедливо соотношение

Таким образом, используя Р(А), определим апри­орные шансы А

и апостериорные шансы А при получении доказатель­ства Х

                                     .                                    (6.1)

При этом вероятность Р и шансы О связаны отно­шением

                                                                                                             (6.2)

если определены шансы, то можно получить вероят­ность. Пусть

 -

отношение правдоподобия при получении доказатель­ства X, отсюда  следует

                                                  .                                                  (6.3)

Аналогично если определить отношение правдоподо­бия λ_у относительно доказательства Y, то получим апостериорные шансы А при выводе из независимых доказательств Х и Y

                                                        .                                           (6.4)

Априорную вероятность Р(А) гипотезы А (или априорные шансы О(А)) и правдоподобные отноше­ния λ_x, λ_у приписанные правилам, задаются на основе знаний эксперта. Если одно из доказательств Х или Y, либо оба подтверждаются с вероятностью 1, то из формул, (6.1) и (6.2) соответственно можно определить апостериорные шансы и апостериорную вероят­ность А, но если доказательства включают ненадеж­ные данные, то применяют следующий приближенный метод.

Пусть известно (из предыдущих выводов), что доказательство Х справедливо с вероятностью Р(Х | •) со значением в отрезке [0, 1]. Тогда апостериорную ве­роятность Р(А | (Х | •)) гипотезы А можно задать, на­пример, как функцию, указанную на рис. 6.9. То есть если доказательство подтверждается с вероятностью, меньшей априорной вероятности Р(Х), то соответ­ствующее правило ничего существенно не дает и не влияет на дальнейшие выводы,  но если вероятность больше Р (X), то влияние задается  линейной

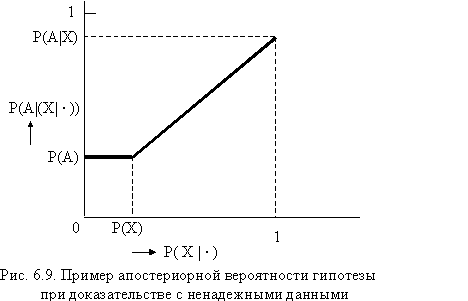
функ­цией. При этом эффективное отношение правдоподо­бия определяется следующим образом:

Для доказательства Y можно определить анало­гичное эффективное отношение правдоподобия . Из сказанного выше следует, что при выводах в случае ненадежных доказательств можно руководствоваться следующими правилами. Если есть только доказательство X, то λ_x в формуле (6.3) заменяется на :

а если одновременно существует независимое доказа­тельство Y, то λ_у в формуле (6.4) заменяется на :

.

Это и есть субъективный байесовский метод.

Здесь возникает проблема: что делать, когда сум­ма вероятностей подмножеств, для некоторой подцели, взаимно опровергающих друг друга, не равна 1 ? Впрочем, в этом случае можно нормировать вероятно­сти. Но кроме этой проблемы существуют проблема необходимости заранее устанавливать априорные ве­роятности каждого условия, проблема соответствия действительности функции на рис. 6.9 и другие про­блемы.                    |

Метод выводов на основе теории Демпстера-Шафера

 

Есть одно существенное критическое замечание по поводу представления ненадежности байесовской ве­роятностью, зависящей от субъективного мнения че­ловека, эта вероятность не позволяет эффективно опи­сать незнание. Другими словами, для байесовской ве­роятности требуется соотношение Р(А)+Р(Ā)= 1, поэтому нельзя отделить отсутствие доверия от недо­верия. И то и другое выражается через Р(А).

Для представления субъективной ненадежности, которую не способна выразить байесовская вероят­ность, Демпстер предложил такие поня­тия, как нижняя и верхняя вероятности. Шафер, совер­шенствуя теорию Демпстера, переименовал их, соот­

ветственно, в функцию доверия и меру правдоподобия с целью придания этим понятиям субъективного смыс­ла. Ниже в общих чертах познакомимся с теорией Демпстера —

Шафера и опишем метод ее применения к выводам в инженерии знаний.

Нижняя и верхняя вероятности определяются с по­мощью базовой вероятности. По Шаферу базовая вероятность m(A_i) «замыкается» в подмножестве A_i, и можно представить ее образ как «полуподвижную вероятностную массу», свободно перемещающуюся по всем точкам внутри А; (рис. 6.10). Этот образ — ключ к пониманию такой вероятности. Пусть А₀ - ограни­ченное множество, a A_i ((i = 1, 2, …) его подмножества, тогда базовая вероятность определяется через функцию m, удовлетворяющую следующим условиям:

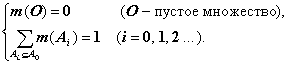
Степень незнания представляется через базовую вероятность m(А₀) полного множества, т. е. это ба­зовая вероятностная масса, местонахождение которой не определено. При m(А_i) < 0 А_i называется цен­тральным элементом.

Нижнюю вероятность можно определить с по­мощью базовой вероятности следующим образом:

                                                                                                  (6.5)

Иначе говоря, это сумма базовых вероятностей, за­мкнутых в подмножестве А_i и не выходящих за него. С другой стороны, верхняя вероятность определяется как

То есть, это сумма базовых вероятностей, которые хотя бы частично могут войти в А_i.

Главное правило — правило комбинации Демпстера (рис. 6.11). Пусть m₁ и m₂ — базовые    вероятности гипотезы, полученной из независимых доказательств, а А_1i и А_2j  (i, j = 0, 1, 2, …) — соответствующие центральные элементы, тогда правило комбинации Демпстера задает новую базовую вероятность, которую можно представить следующей формулой:

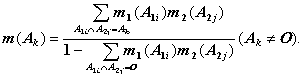                                                          (6.6)

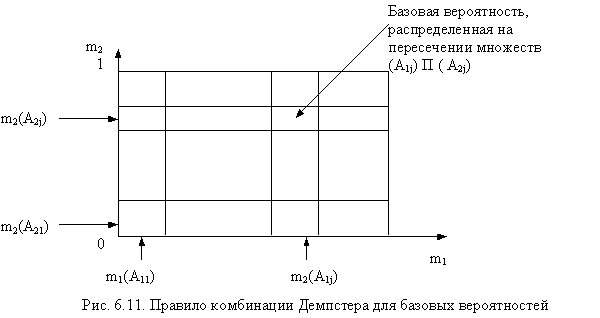Числитель в этой формуле означает, что произве­дение соответствующих базовых вероятностей распре­деляется на пересечение А множеств А_1i и А_2j , как указано на   рис. 6.11, а знаменатель нормирует это произведение, если исключить случай, когда пересече­ние множеств А_1i и А_2j есть пустое множество, то есть случай комбинации противоречащих друг другу выво­дов (существует мнение, что такое нормирование де­лать не нужно). Если в случае двух и более базовых вероятностей они получаются из независимых доказательств, то целевую вероятность можно представить путем последовательного применения формулы (6.6).

Один из методов применения теории Демпстера — Шафера к выводам в инженерии знаний состоит в следующем. Пусть выводы в правилах 1 и 2 на рис. 6.8, в — это два различных подмножества A₁ и A₂, не являющиеся одним и тем же подмножеством пол­ного множества A₀.

Правило 1.       ЕСЛИ Х

                          ТО       А₁, с С₃₁.

Правило 2.       ЕСЛИ Y

                          ТО       А₂, с С₃₂.

Пусть в общем случае С_{правила} — степень надежно­сти, приписанная правилу, если заведомо выполняется предпосылка, тогда это есть базовая вероятностная масса (со значением в [0, 1]), распределенная на под­множество, указанное в выводе правила.

При выводе, прежде всего, вычисляется по формуле (6.5) нижняя вероятность предпосылки. Если в предпосылку входят связи И и ИЛИ, как указано на рис. 6.8, то берутся минимальные и максимальные значения соответствующих нижних вероятностей. За­тем они умножаются на С_{правила}, и полученное значе­ние считается базовой вероятностью подмножества, записанного в выводе правила. Если m₁ — базовая ве­роятность гипотезы A₁, которая получается из правила 1 и доказательства X, то

m₁(A₁) = P_*(X) • C₃₁.

Аналогично из правила 2 и доказательства Y выво­дится m₂(A₂). Распределение базовых вероятностей, выводимых из доказательств Х и Y, связанных через КОМБ, получается из формулы (6.16).

Теория Демпстера — Шафера основана на понятии множества, и если допустить, что подмножества, по­являющиеся в фактических знаниях, имеют общие части, то реализация положений этой теории как универсального средства обработка знаний стано

вится сложной. Однако если ограничиться взаимно не перекрывающимися подмножествами, то все оказывается сравнительно просто. Множества с неопределенными границами можно обрабатывать как нечеткие множе­ства, и понятие множества в теории Демпстера — Шафера можно расширить так, чтобы в него входили нечеткие множества.

Нечеткая логика

Нечеткая логика, выделившаяся из теории нечет­ких множеств, — это разновидность непрерывной ло­гики, в которой логические формулы могут принимать истинностные значения между 1 и 0. Можно обсу­ждать глубокую связь между многозначной и непре­рывной логикой, но в данном разделе будут рассмо­трены только аспекты ее использования в современной инженерии знаний.

В нечеткой логике достоверность представляется как истинностное значение между 1 и 0, и значения, приписанные правилам на рис. 6.8, это и есть истин­ностные значения (вероятность определяется в стати­стическом смысле, и в отличие от нее истинностное значение — это некоторое произвольное субъективное значение, не имеющее никакого статистического смыс­ла). Пусть t_x и t_y - истинностные значения предпосы­лок Х и Y некоторого правила, тогда истинностное значение t_{предпосылки} в случае связей И и ИЛИ на рис. 6.8, а, б определяется следующим образом.

1) При связи И

t_{предпосылки} = min { t_x, t_y}.

2) При связи ИЛИ

t_{предпосылки} = max { t_x, t_y }.

Если в общем случае t_{правила} есть истинностное значение, приписанное правилу, то истинностное значение t_A, распределенное на вывод, определяется как

t_A = min {t_{предпосылки}, t_{правила}).

Определение минимума — это идея, свойственная не­четкой логике и отличающая ее от других методов (в которых производится умножение). Связь КОМБ на рис. 6.8 особо не оговаривается. В качестве такой связи можно рассматривать одну из связей И или ИЛИ. Собственно говоря, в нечеткой логике и нечет­ких выводах рассматривается случай, когда множе­ства X, Y, А и другие, описанные в предпосылках и выводах правил, суть нечеткие множества.

Вероятностная логика

Нильсон предложил идею расширения логики и ввел понятие вероятностной логики, в которой всем логическим формулам приписывается вероятность. Здесь вероятность вновь соответствует законам Байеса. Связь логики и вероятности важна также с точки зрения рационального построения новой теории на ос­нове теории логического моделирования. И хотя эта теория еще не доведена до использования на уровне вычислений, ознакомимся с ней на простых примерах.

Рассмотрим три логические формулы в логике вы­сказываний: А, А EВ, В. Представим следующие вертикальные векторы:

1 2 3 4

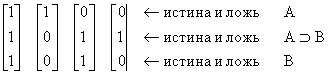
где    1 — мир истинности А, А É В, В,                

2 — мир истинности А и лжи А É В, В,     

3 — мир лжи А и истинности А É В, В,

4 — мир лжи А, В и истинности А É В.

А именно, 1 и 0 обозначают истину и ложь высказы­вания А в первой строке вертикальных векторов, А É В во второй строке и В в третьей строке. Эти три логиче­ские формулы подобраны так, что возможны только четыре указанных выше случая (когда нет противоречия). Это так называемые возможные миры (миры с возможностью интерпретации). Все другие миры — например А, А É В истина, В ложь — это миры, со­держащие противоречие.

Если выбрать один из возможных миров, то обра­зуется традиционная двузначная логика. В вероят­ностной логике рассматриваются состояния, когда одновременно с некоторой вероятностью могут суще­ствовать несколько возможных миров. Например, пусть вероятность, с которой возможна интерпретация в мире 1, равна 0,4, а вероятности интерпретации в мирах 2,3,4 соответственно равны 0,3, 0,2, 0,1 (сум­ма вероятностей возможных миров равна 1), тогда представим следующим образом вектор вероятностей возможных миров:

.

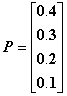И наоборот, если существует группа логических формул, каждой из которых приписана некоторая ве­роятность, то эту группу можно считать упорядочен­ной (непротиворечивой), только когда возможно ве­роятностное существование соответствующих возмож­ных миров. В данном примере это заштрихованная область на рис. 6.12.

Если построить матрицу М, элементами которой служат вертикальные векторы, представляющие воз­можные миры, то с помощью матричной операции МР = V можно вычислить вероятности выбора каж­дой логической формулы. В данном примере

.

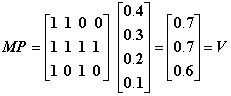А именно, эти вероятностные возможные миры имеют состояние «истина» с вероятностью 0,7 (А),  0,7 ,(А É В) и 0,6 (В).

Пусть задана вероятность А р(А) и вероятность А É В р(А É В), тогда вероятность В р(В) должна находиться в диапазоне

Таким образом, можно определить логический вывод (с вероятностью).

Один из методов однозначного определения веро­ятности логического вывода предполагает, что воз­можные миры имеют распределение вероятностей с возрастающей энтропией. Остаются еще проблема объема вычислений при большом числе логических формул и много других проблем, но, тем не менее, это является важной идеей в рациональном слиянии логики и вероятности.