Генетические алгоритмы – не единственный способ решения задач оптимизации. Кроме него существуют два основных подхода для решения таких задач – переборный и локально-градиентный, каждый из которых имеет свои достоинства и недостатки.

Сравним стандартные подходы с генетическими алгоритмами на примере задачи коммивояжера (TSP – TravellingSalesmanProblem), суть которой состоит в нахождении кратчайшего замкнутого пути обхода городов, заданных своими координатами.

Уже для 30 городов поиск оптимального пути представляет собой сложную задачу, побудившую развитие новых методов (в том числе нейронных сетей и генетических алгоритмов).

Каждый вариант решения (для 30 городов) – это числовая строка, где на j-м месте стоит номер j-го по порядку обхода города. Таким образом, в этой задаче 30 параметров, причем не все комбинации значений допустимы.

Переборный метод наиболее прост в программировании. Для поиска оптимального решения (максимума целевой функции) требуется последовательно вычислить значения целевой функции во всех возможных точках, запоминая максимальное из них. Недостатком метода является большая вычислительная сложность: требуется просчитать длины более вариантов путей, что совершенно нереально. Однако, если перебор всех вариантов за разумное время возможен, то найденное решение является оптимальным.

Второй подход основан на методе градиентного спуска. Вначале выбираются некоторые случайные значения параметров, а затем эти значения постепенно изменяют, добиваясь наибольшей скорости роста целевой функции. При достижении локального максимума такой метод останавливается, поэтому для поиска глобального оптимума требуются дополнительные меры.

Градиентные методы работают быстро, но не гарантируют оптимальности найденного решения. Они идеальны для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный максимум (он же – глобальный). Однако задача коммивояжера таковой не является.

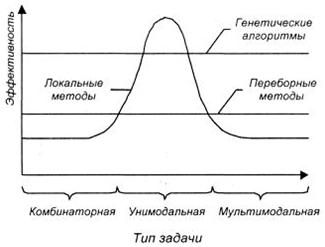
Рис. 6.2. Эффективность генетических алгоритмов

Практические задачи, как правило, мультимодальны и многомерны, т.е. содержат много параметров. Для них не существует универсальных методов, позволяющих достаточно быстро найти абсолютно точные решения. Комбинируя переборный и градиентный методы, можно получить приближенные решения, точность которых будет возрастать с увеличением времени расчета.

Генетический алгоритм представляет собой именно такой комбинированный метод. Механизмы скрещивания и мутации в каком-то смысле реализуют переборную часть метода, а отбор лучших решений – градиентный спуск. На рис. 6.2 показано, что такое сочетание обеспечивает устойчиво хорошую эффективность генетического поиска для любых типов оптимизационных задач.

Таким образом, если на некотором множестве задана сложная функция от нескольких переменных, то генетический алгоритм за разумное время находит значение функции, достаточно близкое к оптимальному. Задавая время расчета, можно получить одно из лучших решений, которые реально получить за это время.