Одновременность событий в разных системах отсчета
а) Если в системе ![]() в координатах
в координатах ![]() и
и ![]() происходят два события в моменты времени
происходят два события в моменты времени ![]() и
и ![]() .В системе
.В системе ![]() им соответствуют координаты
им соответствуют координаты ![]() и
и ![]() и моменты времени
и моменты времени ![]() и
и ![]() .
.
Если в системе ![]() события происходят в одной точке
события происходят в одной точке ![]() и одновременно
и одновременно ![]() , то согласно формуле (6.1):
, то согласно формуле (6.1):![]() и
и ![]() , то есть эти события являются одновременными и пространственно совпадающими для любой инерциальной системы.
, то есть эти события являются одновременными и пространственно совпадающими для любой инерциальной системы.
б) Если события в системе ![]() пространственно разобщены
пространственно разобщены ![]() , но одновременны
, но одновременны ![]() , то в системе
, то в системе ![]() согласно формуле (6.1)
согласно формуле (6.1) ![]() и
и ![]() .
.
Таким образом, эти события, оставаясь пространственно разобщенными оказываются и неодновременными.
Длительность событий в разных системах отсчета
Если длительность события в системе ![]() выражается
выражается ![]() ,то длительность этого же события в системе
,то длительность этого же события в системе ![]() :
:![]() .
.
Из преобразований Лоренца следует:![]() , то есть
, то есть ![]() , иначе длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
, иначе длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
Длина тел в разных системах отсчета.
Пусть в системе ![]() вдоль оси
вдоль оси ![]() покоится стержень. Длина стержня в системе
покоится стержень. Длина стержня в системе ![]() будет
будет ![]() . Определим длину этого же стержня в системе
. Определим длину этого же стержня в системе ![]() , относительно которой он движется со скоростью
, относительно которой он движется со скоростью ![]()
Используя преобразования Лоренца, получим:![]() .
.
Таким образом длина стержня![]() , измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой он покоится.
, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой он покоится.
Релятивистский закон сложения скоростей
Пусть материальная точка движется в системе ![]() со скоростью
со скоростью ![]() , а сама система движется относительно системы
, а сама система движется относительно системы ![]() со скоростью
со скоростью ![]() .
.
Релятивистский закон сложения скоростей имеет вид:
![]()
![]()

Если материальная точка движется параллельно оси ![]() , то скорость
, то скорость ![]() относительно системы
относительно системы ![]() совпадает со скоростью
совпадает со скоростью ![]() , а скорость
, а скорость ![]() относительно
относительно ![]() совпадает со скоростью
совпадает со скоростью ![]() . Тогда сложения скоростей примет вид:
. Тогда сложения скоростей примет вид:
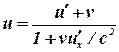
![]() .
.