Полностью описать мир задач чрезвычайно слож­но. Например, знание «птицы  летают» — верное, од­нако встречаются и нелетающие птицы, т. е. это не­полное значение. В области искусственного интеллекта изучают задачу «миссионер и туземцы» — это задача о переправе через реку на одной лодке. Но если вдруг нет весел или на дне лодки дыра, задача ста­новится неразрешимой. Подобных причин может быть множество, а раз так, то полностью описать их невоз­можно. Исходя из здравого смысла, считают, что раз существует лодка, то ею можно пользоваться.

Другой пример: можно перечислить все предметы, которые находятся в комнате, но того, чего в ней нет, перечислить невозможно, поскольку это бесчисленное множество предметов. Точно так же можно перечис­лить верные знания (в некоторой проблемной обла­сти), но перечислить неверные знания и разумно их определить невозможно. Поэтому удобно в базе зна­ний определять исключительно верные знания, а все, что не определено, считать заведомо неверным. Утвер­ждения, которые не упомянуты ни как истинные, ни как ложные, принято относить к ложным. Это назы­вают гипотезой закрытого мира. Предикат not в язы­ке Пролог принимает значение «истина», если среди его аргументов нет решения, и его выполнение осно­вано на гипотезе закрытого мира. Эта же гипотеза нередко применяется для неопределенных знаний (разновидности неполных знаний). Классическая ло­гика исходит из предпосылки, что набор определен­ных в ней аксиом (знаний) полон, и правильный вы­вод не меняется, даже если впоследствии добавлена новая аксиома. Такое свойство называется монотон­ностью. Если допустить, что в базу знаний добавлено такое знание: «как правило, птицы летают (за неко­торым исключением)», то обнаружится свойство не­монотонных выводов. А именно, при добавлении новой аксиомы иногда возможно отрицание вывода, ко­торый считался верным в некоторой системе аксиом (базе знаний).

Введем обозначение М, а Мр будет означать, что «логическая формула р непротиворечива (по отноше­нию к другим знаниям)» (другими словами, «Мр истинно, если из других знаний не получается вывод ┐ р»). При этом знание «как правило, птицы летают (за некоторым исключением)» можно представить в виде следующей логической формулы:

(х)      птица (х) / М летает (х) É летает (х).

              {смысл: х — птица, х летает, если летать не противоречит (другим

                знаниям)}

Теперь рассмотрим систему аксиом, состоящую из следующих знаний:

(х)      птица (х) / М летает (х) É летает (х).

(x)      пингвин (х) É ┐ летает (х).

              птица (Пикколо).

Из этой системы аксиом можно сделать вывод «ле­тает (Пикколо)», то есть Пикколо (кличка пингвина) летает. Однако впоследствии получена более по­дробная информация, выяснилось, что Пикколо — это пингвин. И в систему аксиом внесено добавление Пингвин (Пикколо). Теперь вывод, полученный ранее «летает (Пикколо)», отрицается и делается новый вывод: «┐летает (Пикколо)». Это пример немонотон­ности выводов. Как средство формальной обработки неполных знаний, при которой необходимы немоно­тонные выводы, предложены и активно исследуются методы немонотонной логики. Типичные подходы: не­монотонная логика Макдермотта и Доула (в которой вводятся условные логические операции), логика умолчания Рейтера, окружение (circumscription) (в смысле ограничения) Маккарти и др. Маккарти из­вестен как создатель языка Лисп, он всячески под­черкивает, что в дополнение к знаниям, которые в настоящее время стали объектом обработки компью­теров, необходимо сделать скачок к тому, что мы на­зываем здравым смыслом. По его словам, это самая большая проблема искусственного интеллекта, и в ней не обойтись без немонотонных выводов.

В немонотонной логике Макдермотта и Доула, ло­гике умолчания Рейтера, как мы видим из примеров, введено логическое обозначение М, и Мр означает, что «логическая формула р не противоречива (по от­ношению к другим знаниям)». Основная проблема, которая возникает при включении подобных знаний, может быть сведена к следующему. Пусть в базе зна­ний (системе аксиом) существуют знания (логические формулы) {Мр É ┐ q, Mq É ┐ р}. Тогда для решения возникают две возможности: {решение, которое вклю­чает ┐р, но не включает ┐q, и решение, которое включает ┐q, но не включает ┐р, то есть решение определяется неоднозначно. При этом нельзя сделать вывод о том, может ли ┐р или ┐q являться реше­нием. Как говорят, не определена неподвижная точка; исследования этой серьезной проблемы продол­жаются.

Немонотонная логика еще полностью не изучена, но функции значений по умолчанию уже находят практическое применение, например, в представлении фреймов. В таких случаях используют метод, позво­ляющий однозначно определять значения в зависимо­сти от способа вывода. Например, есть база фреймов, указанная на рис. 6.13, и задан вопрос «способен ли летать Пикколо?», но атрибут понятия «летать» не определен во фрейме ПИККОЛО, поэтому обратимся к фрейму ПИНГВИН, на который ссылает нас указа­тель IS-A. В нем есть определение «не летает», по­этому окончательный ответ «нет». Здесь же указатель IS-A отправляет нас к фрейму ПТИЦА, где по умол­чанию определено значение «да», но предпочтение от­дается значению в слоте фрейма ПИНГВИН, откуда была последняя ссылка.

К системам, связанным с неполными знаниями и управлением такими знаниями, относится система поддержания значений истинности. В базе знаний этой системы, неполной и содержащей противоречия, все знания делятся на достоверные и недостоверные, и предусмотрено упорядочение базы с целью устране­ния недостоверных знаний. В этой системе достоверно истинные знания относятся к классу «IN», а знания, истинность которых недостоверна либо в истинность которых нет повода верить, — к классу «OUT». Если при добавлении новых знаний возникает противоре­чие, то выполняется повторная проверка классов зна­ний. Аналогичные функции реализованы в системе   

ло­гического программирования, разработанной в ICOT, они названы функциями координации и поддержания равновесия знаний.

Логика умолчания

Несколько слов скажем и о логике умолчания Рейтера как примере немонотонной логики.

ПТИЦА

              (ЛЕТАЕТ по умолчанию: да)

              (ИМЕЕТ крылья)

ЛАСТОЧКА

              (IS-A    ПТИЦА)

ПИНГВИН

              (IS-A    ПТИЦА)

              (ЛЕТАЕТ нет)

ПИККОЛО

              (IS-A   ПИНГВИН)

Формат фрейма приведен ниже, слот IS-A указывает фрейм верхнего уровня, из которого наследуются свойства.

   Название фрейма

                   (Название слота (по умолчанию) значение слота)

Рис. 6.13. Пример базы фреймов, содержащей значения по умол­чанию

Если в монотонной логике Макдермотта и Доула атомарные формулы со знаком М могут записываться в произ­вольном месте правильно построенных логических формул (ппф), то в логике умолчания Рейтера они используются только в предпосылках правил вывода.

Рассмотрим запись формулы

Птица (х): М летает (х)

         летает (х)

Она означает: «птица (х) / М летает (х) É летает (х)», то есть «х — есть птица, х летает, если это не противоречит (другим знаниям)». Предпосылка правила запи­сана над чертой, она делится знаком « : » на две части: формула без знака М и формула со знаком М. Таким образом вводится ограничение на расположение фор­мул со знаком М. Как отмечалось выше, при этом воз­можно несколько решений и возникают ситуации, когда решение нельзя определить однозначно; соответ­ствующее решение рассматривается как один из воз­можных миров и называется «вытяжкой» (extension) из системы аксиом. Переход от одного выбранного ре­шения к другому рассматривается как переход между возможными мирами. Правила выводов со знаком М кратко называют правилами умолчания. Общая фор­мула

.

Запись, в которой формула после знака М в пред­посылке совпадает с формулой в выводе, называется нормальным умолчанием. В большинстве случаев зна­ния по умолчанию можно представить в такой форме. Запись нормального умолчания, в которой не содержат свободных переменных, называется за­крытым нормальным умолчанием. Если все умолча­ния — это закрытые нормальные умолчания, то можно показать, что такая система знаний имеет, по меньшей мере, одну вытяжку (возможный мир).

Рейтер определил процедуру доказательства того, включается ли некоторая формула в одну из вытяжек из системы, содержащей нормальные умолчания (су­ществует ли теорема, которую можно вывести из этой системы). Приведем эту процедуру для логики выска­зываний. Пусть система, содержащая нормальные умолчания, определена так, как на рис. 6.14, где D -  множество формул нормального умолчания, W —  мно­жество формул, не являющихся умолчанием, а сама система есть совокупность (D, W). Тогда рассмотрим доказательство: включается ли Е в одну из вытяжек.

Используем линейный вывод сверху — вниз по прин­ципу от противного, допустим, что справедливо отри­цание искомой формулы ┐Е, и придем к противоре­чию     (если при методе приведения к абсурду приходят к противоречию, то, как логическое следствие, в дан­ном случае считают, что Е включается в одну из вы­тяжек (возможный мир)). Запишем ниже основные этапы этого метода. Обозначим через ПРЕДПОСЫЛ­КИ (D_i)  (i = 0,1,2, ….k) логические формулы без знака М (слева от знака « : ») в предпосылках подмножеств D_i умолчаний, а через ВЫВОДЫ (D_i) — формулы в выводах D_i.

Прежде всего, возьмем подмножество D₀ множе­ства D и множество W и докажем методом приведе­ния к противоречию, что Е можно вывести из W È ВЫВОДЫ (D₀).

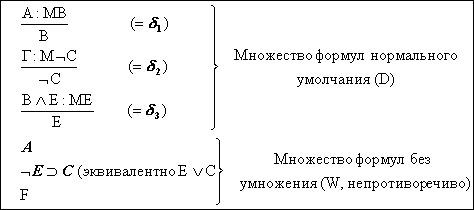
Рис. 6.14. Пример системы, содержащей нормальные умолчания (определяется

как совокупность (D,W))

При этом должны быть справедливы ПРЕДПО­СЫЛКИ (D₀), поэтому возьмем подмножество D₁ множества D и аналогично докажем тем же методом, что ПРЕДПОСЫЛКИ (D₀) выводятся из W È ВЫ­ВОДЫ (D₁).

Далее  докажем  ПРЕДПОСЫЛКИ (D₁) из W È ВЫВОДЫ (D₂) и так далее и будем повторять доказательства до получения D_k = 0 (пустое множе­ство).

В конце концов придем к заключению, что

 удовлетворяет (не противо­речит) допущению.

Но если это так, то можно доказать, что искомая формула включается в одну из вытяжек.

На рис. 6.15, а, б показаны два этапа доказатель­ства с помощью данного метода, Е включается в вытяжку из системы на рис. 6.14.

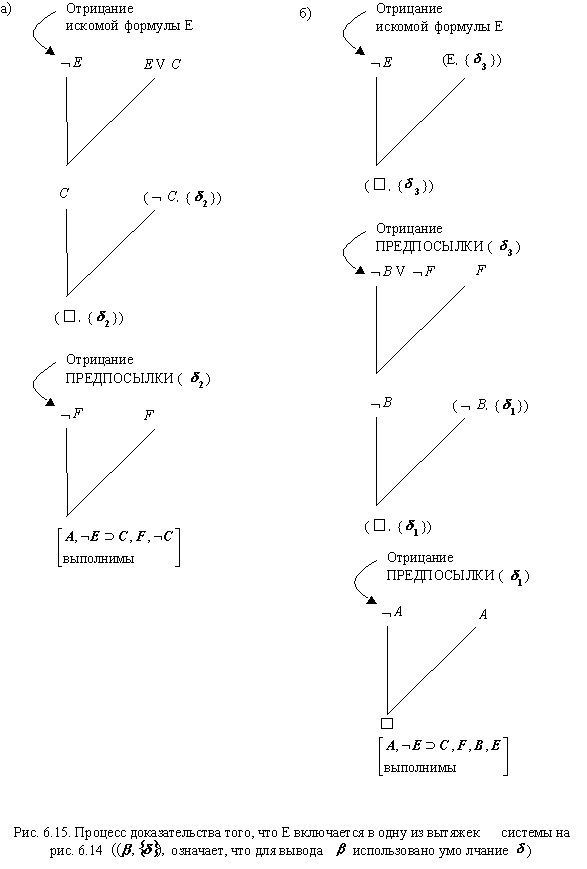
Немонотонная логика, как и логика умолчания, еще содержит немало проблем, но она важна как логическое обоснование обработки неполных знаний, поэтому изучается очень активно.