Если задана формула ![]() , то можно использовать формулы остаточных членов (погрешности):
, то можно использовать формулы остаточных членов (погрешности):
![]() ,
,
![]() ,
,
![]() .
.
Либо можно использовать правило Рунге. Считаем ![]() и
и ![]() , затем находим погрешность
, затем находим погрешность ![]() .
.
Если формула ![]() не задана, то используем правило Рунге. Считаем
не задана, то используем правило Рунге. Считаем ![]() , а затем
, а затем ![]() (то есть считаем, что часть
(то есть считаем, что часть ![]() нам неизвестна).
нам неизвестна).

Рис.6.6. Оценка погрешности по правилу Рунге
Пример
Рассмотрим формулу трапеций при ![]() и
и ![]() .
.
В данном случае погрешность численного интегрирования ![]() равна модулю разности площадей двух заштрихованных треугольников, деленной на три (рис. 6.6).
равна модулю разности площадей двух заштрихованных треугольников, деленной на три (рис. 6.6).
Как определить число n элементарных отрезков, на которые необходимо разбить отрезок ![]() , для того, чтобы достичь точности e? Рассмотрим на примере формулы трапеций.
, для того, чтобы достичь точности e? Рассмотрим на примере формулы трапеций.
![]() ,
, ![]() .
.
![]() ,
, ![]() ,
,
![]() ,
, 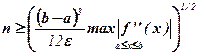
Отметим, что полученное число ![]() является, как правило, заметно завышенным.
является, как правило, заметно завышенным.