Все составные квадратурные формулы, которые мы рассматривали, записывались для случая равномерного шага. Мы также разобрали, как определить число равных отрезков n, на которые необходимо разбить отрезок , для достижения точности e.

Но на практике часто используют неравномерный шаг при численном интегрировании. Почему? Для экономии числа арифметических действий. Неравномерный шаг позволяет резко сократить объем вычислений при той же точности вычислений.

При оценке эффективности программ для численного интегрирования обычно предполагают, что большая часть стоимости счета приходится на вычисление значений подынтегральной функции . Использование неравномерного шага и позволяет резко сократить число интервалов и, следовательно, число значений функции , которые необходимо находить. Но в этом случае должна быть задана формула функции  либо алгоритм для вычисления значения  в любой точке отрезка /13/.

Рассмотрим алгоритм вычисления интеграла 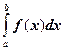  , где  может быть вычислено для любого  из отрезка [a, b] с заданной точностью.

При интегрировании с неравномерным шагом реальное число интервалов, их расположение и длины зависят от функции  и требуемой точности e.

В этом случае сначала вычисляется приближённое значение  на отрезке ,  . Затем отрезок делится пополам, и вычисляется  на этом же отрезке, но в два этапа. Оценивается погрешность по правилу Рунге. Если погрешность удовлетворяет неравенству: 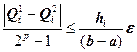  ,   то переходим к следующему отрезку, в противном случае снова делим отрезок пополам и т.д.