Прямоугольная таблица, составленная из mxn элементов a_ii (i = 1,2,3,…n; j = 1,2,3,…m) некоторого множества, называется матрицей размера mxn.

Матрицы обозначают большими латинскими буквами А, В… Например:

.

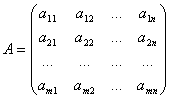Элементы а₁₁, а₁₂,…, а_1n  образуют первую строку; а_11, а₂₁,…,а_m1 – первый столбец. Строки и столбцы называют рядами. Произвольный элемент матрицы обозначают a_ij. Краткая форма записи матрицы:  (a_ij)_mn, а числа i, j называют индексами элемента. Элементы а_11,  a_22, …,a_mn  образуют главную диагональ матрицы.  Если m = n, то матрица  называется квадратной.

Две матрицы (а_ij)_mn и  (b_ij)_pq называют равными, если  p = m, q = n  и a_ij = b_{ij ,} то есть они одних размеров и их соответствующие элементы равны.

Матрица, состоящая из одной строки или одного столбца, соответственно называется матрицей-строкой или матрицей-столбцом.

Матрица, всё элементы которой равны нулю, называется нулевой и обозначается буквой О.

Порядком матрицы называется число её строк (для квадратной матрицы).

Квадратная матрица называется симметрической, если а_ij = a_ji.

Диагональной матрицей называется квадратная матрица, у которой все элементы не принадлежащей главной диагонали равны нулю, и обозначается символом:

.

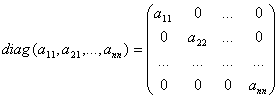Единичной называется диагональная матрица, все элементы главной диагонали которой равны единице, и обозначается Е или I:

.

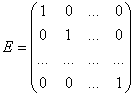Матрица, полученная из данной матрицы А заменой каждой её строки соответствующим  столбцом, называется транспонированной и обозначается А^Т.

, .

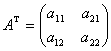Например:

, .

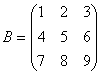Линейные операции над матрицами

К линейным операциям относятся: сложение и вычитание матриц, умножение матрицы на  число. Сложение и вычитание определяется только для матриц одинаковых размеров.

Суммой (разностью) матриц А = (а_ij)_mn и В = (b_ij)_mn называется матрица С = (с_{ij =} а_ijb_ij). Например, если

, , .

Произведением матрицы А = (а_ij)_mn на число  называется матрица:

В = А   В = (а_ij)_mn,

то есть каждый элемент матрицы А умножается на число .

Произведение матриц

Произведение определяется для квадратных матриц одного и того же порядка, а также для прямоугольных матриц, у которых число столбцов множимого равно числу строк матрицы множителя. Обозначается:

С = , т.е., если А = (а_ij)_mn ,  В = (b_ij)_nl, то С_ml = (С_ij)_ml ,

где                                                    С_ij = а_i1 b_1j + а_i2 b_2j+…+ а_in b_nj =

(элемент матрицы С_ij  равен сумме произведений элементов i-строки матрицы А на соответствующие элементы j-го столбца матрицы В). Заметим, что не всегда =.

Например:

,      .

Определители. Минор и алгебраическое дополнение

Определители вводятся для квадратных матриц.

Определителем квадратной матрицы второго порядка называется число, равное а₁₁а₂₂ - а₁₂а₂₁,  обозначается символом:

.

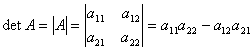Имеют место свойства определителей и теоремы, которые касаются их вычисления.

Определителем квадратной матрицы А = (а_ij)_3x3  (третьего порядка) называют число:

.

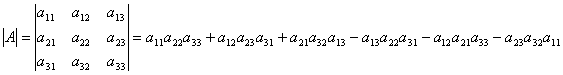Правило знаков:

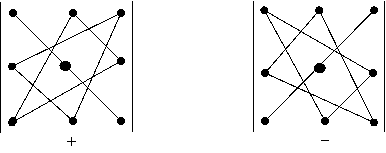
Минором элемента a_ij определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Минор элемента a_ij обозначается М_ij.

Алгебраическим дополнением элемента a_ij определителя называется его минор, взятый со знаком (-1)^i+j,  обозначается символом A_ij:

.

Для определителей вводится понятие порядка "по принципу порядка матрицы".

Если определитель имеет порядок выше трех, то пользуются для его вычисления важным для определителей свойством «разложения» определителя по строке или столбцу.

Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Например:

.

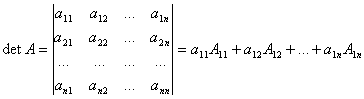Коротко можно записать так:

  — разложение определителя по элементам i-й строки.

На практике часто используют теорему вычисления определителя от произведения матриц. Она утверждает: определитель произведения двух квадратных матриц А и В одного порядка равен произведению определителей перемножаемых матриц:

.

Пример 14. Вычислить определитель по правилу «разложения»:

Объяснения:

1) разложим определитель по элементам четвёртого столбца, который содержит три «нулевых» элемента, которые впоследствии умножаются на алгебраические дополнения (не важно, какие они имеют значения), и за счёт этого имеем выигрыш в  вычислении всего определителя;

2) вычисляем алгебраическое дополнение А₄₄ по правилу треугольника (заметим, что можно было и далее вычислять этот определитель 3-го порядка по правилу разложения, но в целях экономии времени пользуемся правилом, которое знаем для определителя 3-го порядка).

Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Если система является невырожденной, т.е. , то она имеет единственное решение

,

где А^-1- матрица, обратная матрице А, а

.

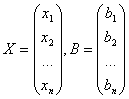Линейные системы уравнений

Линейная система

              ,

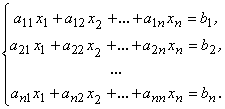
называется невырожденной, если . Тогда эта система имеет единственное решение:

 ;

.

Эти формулы называются формулами Крамера.

Из формул Крамера следует, что если однородная линейная система

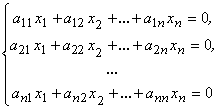
имеет ненулевое решение, то её определитель det А = 0.

Решение однородной системы двух уравнений.

Пусть дана система:

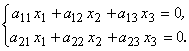
Решения даются формулами:

,

где 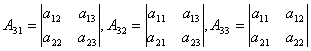 — алгебраические дополнения матрицы 3-го порядка, составленные из коэффициентов при неизвестных данной системы.

Решения однородной системы трех линейных уравнений:

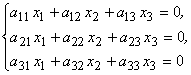
если det А = 0, А₃₃, находятся из подсистемы    по предыдущим формулам (см. предыдущий пункт).

Пример 15: Решить систему с помощью определителей:

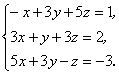
Решение: Найдем det A = 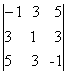=1+45+45-25+9+9=84,

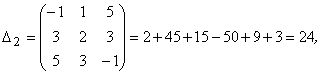
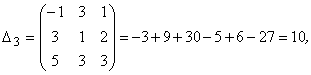
Ответ:                                                      

Пример 16: Решить однородную систему:

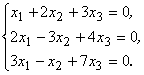
Решение: 1) Найдем det А:

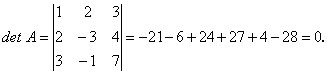
2) Найдем                                       

3) Решим систему:

Решение системы матричным методом

Пусть det А ≠ 0, тогда А×А^-1 = Е; система имеет вид АХ = В, где А – матрица системы; , ;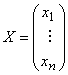

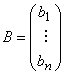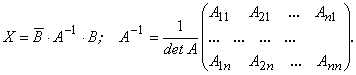
Пример 17: Решить систему матричным методом:

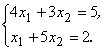
Решение: Матрица системы, матрица-столбец неизвестных и матрица–столбец свободных имеют соответственно вид:

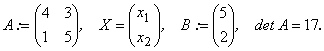
Обратная матрица А^-1 = . Следовательно, матричное решение будет:

.

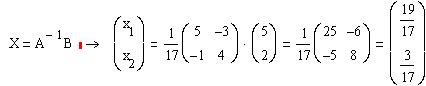Ответ: