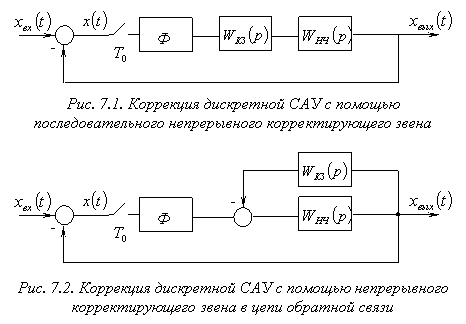
Непрерывные корректирующие устройства, изменяющие НЧ системы, реализуются на практике активными или пассивными фильтрами, которые включаются либо последовательно с НЧ, либо вводятся в контур обратных связей (рис. 7.1, 7.2).

Рассмотрим пример расчета непрерывного последовательного регулятора.

Пример 27

Введение корректирующего устройства в систему (рис. 7.1) с передаточной функцией

и интервалом квантования  должно обеспечивать время регулирования  и перерегулированием .

Дискретная передаточная функция разомкнутой нескорректированной САУ имеет вид:

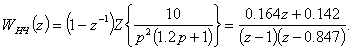
Вводим новую переменную w, осуществляя переход от z-изображений к  w-изображениям:

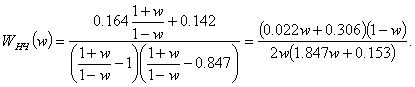
Для построения логарифмических частотных характеристик используем абсолютную псевдочастоту . При  имеем:

Тогда выражение для комплексной амплитудно-фазовой характеристики нескорректированной разомкнутой системы имеет вид:

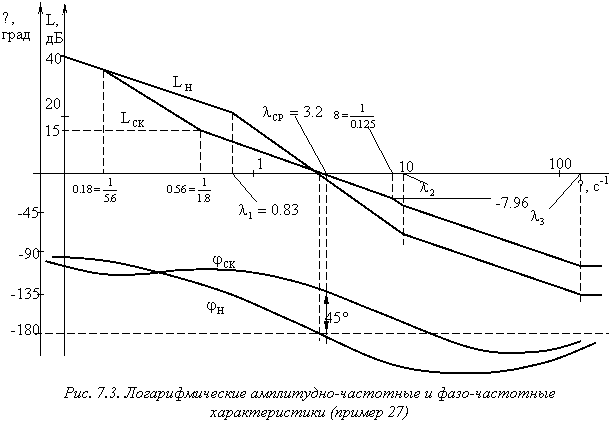Соответствующие этому выражению логарифмическая амплитудно-частотная  и фазо-частотная  характеристики приведены на рис. 7.3. По их виду на основании критерия Найквиста можно сделать заключение, что нескорректированная система находится на границе устойчивости.

Далее необходимо построить логарифмическую амплитудно-частотную  и фазо-частотную  характеристики скорректированной системы, для чего необходимо воспользоваться соответствующими номограммами, разработанными для коррекции непрерывных систем. С их помощью определена частота среза и запас устойчивости по амплитуде для ЛАХ  скорректированной системы:  и дб. Характеристики  и  приведены на рис. 7.3.

Для обеспечения физической реализуемости корректирующего устройства не в полной мере обеспечен требуемый запас устойчивости по амплитуде в высокочастотной части среднечастотного участка ЛАХ. В частотной характеристике скорректированной системы сохранен сомножитель  и введена апериодическая составляющая:

При этом выражение для комплексной амплитудно-фазовой характеристики скорректированной разомкнутой системы имеет вид:

Осуществляя обратную замену , получим:

Используя подстановку , определим дискретную передаточную функцию скорректированной разомкнутой системы в z-форме:

Непосредственно из полученного выражения искомую передаточную функцию корректирующего устройства  определить нельзя. Поэтому воспользуемся тем, что:

Следовательно:

или

.                       (7.1)

Далее необходимо тем или иным способом найти функцию , Z-изображение которой равно выражению, стоящему в правой части равенства (7.1), т.е.:

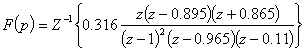
После этого искомая передаточная функция непрерывного корректирующего звена определяется следующим образом:

                                                  (7.2)

В ряде случаев для нахождения функции  достаточно воспользоваться таблицами Z-преобразования. Кроме того, можно применить следующий прием: предварительно найдем решетчатую функцию , Z-изображение которой равно выражению, стоящему в правой части равенства (7.1).

Для рассматриваемого примера

.

Такой решетчатой функции соответствует сколь угодно много непрерывных функций , совпадающих с в моменты квантования. Поэтому переход к  осуществим, формально воспользовавшись равенством:

,

откуда

.

Тогда

.

Изображение по Лапласу от  имеет вид:

Передаточная функция непрерывного корректирующего звена в соответствии с  выражением (7.2) равна: