Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое.

Средняя арифметическая  есть частное от деления суммы всех значений признака на их число. Средняя арифметическая выражается через х и вычисляется по формуле

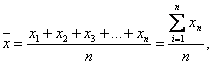
где х₁, х₂, …, х_n – значения признака, n — число наблюдений.

Пусть, например, у нас имеется распределение журналов, выписываемых подписчиками в выборке из 5 человек:

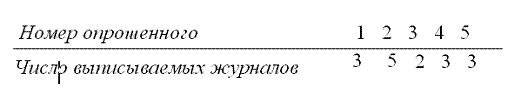
По формуле для  `х находим  `х = ~  3,2 журнала. Такая средняя арифметическая `х называется простой средней и вычисляется обычно в том случае, когда каждое значение признака встречается только один раз. Чаще всего в социологических исследованиях используется взвешенная средняя, когда средняя арифметическая ряда для сгруппированных данных определяется с учетом  весов групп (т.е. их численностей). Формула взвешенной средней

=

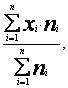
где n_i  — частота для i –го значения признака.

Если находят среднюю для интервального ряда распределения, то в качестве значения признака для каждого интервала условно принимают его середину. Например, вышеприведенный пример о подписке журналов можно сгруппировать следующим образом:

Номер опрошенного                                     3   2   1   4   5

Число выписываемых журналов                 2   5   3   3   3

х:

Частота                                                      1   1   3   —   -

Тогда =.

Недостаток средней арифметической заключается в том, что она затрудняет качественное  сравнение различных групп по данным характеристикам. Это обусловлено тем, что средняя арифметическая  может скрывать за собой различную степень разброса значений. Вычислить этот разброс можно с помощью дисперсии, представляющей собой среднее значение квадрата отклонений отдельных значений признаков от средней арифметической:

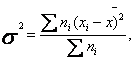
где σ² - дисперсия, х_i - значение признака,   — средняя арифметическая, n_i - частота.

Квадратный корень  дисперсии σ² называется среднеарифметическим отклонением и обозначается S:

Рассмотрим на примере расчет дисперсии. Пусть у нас имеются две группы спортсменов, в которых занимаются соответственно 15 и 20 человек. Посещаемость тренировок в течение двух недель была в первой группе: 13, 14, 15, 15, 13, 14; во вто

рой – 12, 16, 19, 10, 11, 16 человек. Вычислим среднюю посещаемость в первой (₁) и во второй (₂) группах:

₁ =

₂ =

Видно, что среднее значение в обоих случаях одинаково: ₁  = ₂.  Но, с другой стороны, понятно, что во второй группе этот показатель подчинен воздействию каких-то факторов. Вычислим степень разброса значений признака, т.е. дисперсию, предварительно представив отдельные элементы и расчеты в табл. 7.6.

                                                                                                                                 Таблица 7.6

Учитывая, что наш признак “посещаемость” интерпретируется однозначно в каждом из шести случаев, дисперсию можно вычислить аналогично простой средней:

Большее значение дисперсии соответствует и большему разбросу признака (в нашем случае – неравномерности посещения занятий).

Математико-статистические методы все чаще находят применение в современных социальных исследованиях. Тем не менее следует иметь в виду, что статистика с ее методами никогда не может дать полного причинного объяснения отдельным общественным явлениям. Она дает зачастую весьма ценный материал для изучения социальных явлений, однако такое изучение требует также данных, полученных с помощью иных методов и подтвержденных в ходе научного обобщения.

Подробнее вопросы, касающиеся  статистических и количественных методов обработки и анализа  данных  исследования, освещаются в литературе, рекомендованной  к данному пособию.