Известна целая группа методов Рунге-Кутта (в последнее время в отечественной литературе начинает появляться «русский» вариант произношения фамилий авторов метода, а именно метод Рунге-Кутты), среди которых чаще всего используется метод Рунге-Кутта четвёртого порядка.

Идея метода Рунге-Кутта состоит в том, чтобы разностную задачу Коши представить в виде:

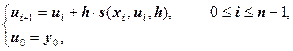
где функция s приближала бы отрезок ряда Тейлора:

с точностью , но в то  же время не содержала бы производных функции . Здесь k – порядок разностной задачи.

Мы рассмотрим методы Рунге первого, второго и четвёртого порядков.

Метод Рунге-Кутта первого порядка (метод Эйлера)

Метод Рунге-Кутта первого порядка – это уже рассмотренная нами явная схема Эйлера (метод Эйлера):

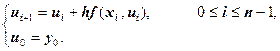
Метод Эйлера – метод первого порядка, то есть локальная погрешность равна , глобальная погрешность равна . Метод Эйлера является одним из самых простых методов, но в практических расчётах используется редко, так как обладает значительной погрешностью. Разностная задача является условно устойчивой. Для модельной дифференциальной задачи Коши:

условие устойчивости разностной задачи .

Метод Эйлера легко обобщается на системы дифференциальных уравнений первого порядка.

Пример

Методом Эйлера построить алгоритм решения задачи Коши:

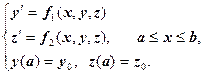
Решение

Запишем разностную задачу:

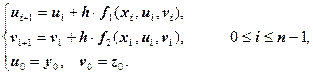
Вектора:  и  являются приближёнными решениями задачи Коши.

Метод Рунге-Кутта второго порядка

Формулы метода Рунге-Кутта второго порядка (метода Эйлера-Коши, модифицированного метода Эйлера) записывается следующим образом:

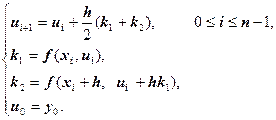
Порядок метода – второй, то есть локальная погрешность равна: , глобальная погрешность . Разностная задача является условно устойчивой. Для модельной дифференциальной задачи Коши:

;

условие устойчивости разностной задачи .

Метод Рунге-Кутта четвёртого порядка

Чаще всего на практике используется метод Рунге-Кутта четвёртого порядка.

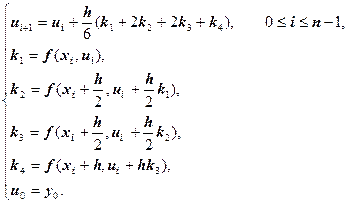
Порядок метода – четвёртый. Локальная погрешность равна: , глобальная погрешность . Разностная задача является условно устойчивой. Для модельной дифференциальной задачи Коши:

условие устойчивости разностной задачи .

Метод Рунге-Кутта четвёртого порядка легко распространяется на системы дифференциальных уравнений первого порядка.

Отметим важное свойство методов Рунге-Кутта. Эти методы являются самостартующими. Самостартующий метод – это численный метод, в котором для начала вычислений не требуется дополнительных расчётов.

Для оценки погрешности методов Рунге-Кутта используют двойной пересчёт на ЭВМ. Сначала находится приближённое решение  на отрезке  с шагом h, а затем расчёт проводится на этом же отрезке в два этапа с шагом h/2, и получается приближенное решение . Величина

,

где k – это порядок разностной задачи, является оценкой погрешности.

При реальных вычислениях используется, как правило, переменный шаг, что позволяет добиться требуемой точности с минимальным количеством узлов сетки. Двойной пересчёт на ЭВМ используется в этом случае как для контроля за погрешностью, так и для определения величины шага.