Задача 1
Функция 
задана таблично:
|
x |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
|
y |
0 |
0.04 |
0.16 |
0.36 |
0.64 |
1.00 |
Вычислить значения первой производной функции y в точках 0., 0.6, 1.0 с первым и со вторым порядком точности по h.
Решение
Для вычисления приближенных значений первой производной с первым порядком по h воспользуемся формулами численного дифференцирования, а именно, формулой дифференцирования вперёд и формулой дифференцирования назад:
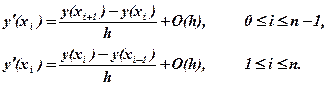
Получаем:
, 
,
.
Отметим, что для вычисления 
с первым порядком по h мы воспользовались формулой дифференцирования вперёд, но можно было воспользоваться формулой дифференцирования назад.
Для вычисления 
во внутренней точке x = 0.6 со вторым порядком по h используется центральная разность:
,
а для вычисления на концах отрезка со вторым порядкм по h применяются формулы:
,
.
Получаем:
, 
, 
Задача 2
Методом Эйлера с шагом h = 0.1 построить алгоритм для решения задачи Коши:
Решение
Запишем разностную задачу Коши:
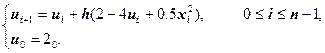
Шаг h = 0.1; значения 
; число 
.
Вектор 
является приближённым решением задачи Коши.
Задача 3
Методом Рунге-Кутта второго порядка с шагом h = 0.1 построить алгоритм для решения задачи Коши:
Решение
Запишем разностную задачу Коши:
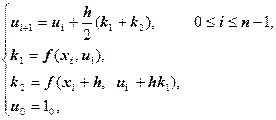
где 
, шаг h = 0.1, 
, 
.
Вектор является приближённым решением задачи Коши.
Задача 4
Методом Рунге-Кутта четвёртого порядка с шагом h = 0.1 построить алгоритм для решения задачи Коши:
Решение
Запишем разностную задачу Коши:
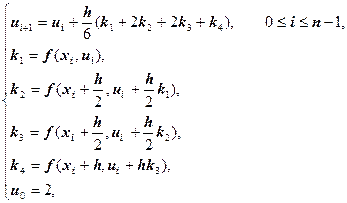
где 
; шаг h = 0.1; ; .
Вектор является приближённым решением задачи Коши.