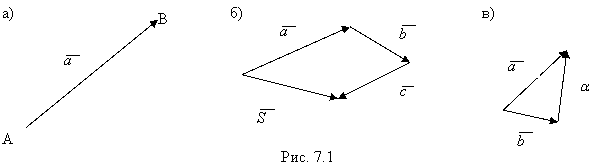
Величина, характеризуемая числовым значением и направлением, называется свободным вектором, или векторной. Геометрически вектор изображается направленным отрезком пространства и обозначается где А – начало отрезка, В – конец его (рис. 7.1).

Под модулем (длиной) вектора  понимается его числовое значение без учета направления.  — нулевой вектор, () не имеет определенного направления.

Два вектора  и  считаются равными, если они расположены на параллельных прямых (или совпадающих) и имеют одинаковую длину и направление. Свободный вектор допускает перенос его в любую точку пространства, при условии сохранения длины и направления.

1) Сумма векторов  есть вектор , который является замыкающим векторной линии со звеньями   (рис. 7.1, б).

2) Разность векторов и  есть вектор , где вектор - противоположный вектору  (рис. 7.1, в), т.е. .

3) Произведением вектора  на скаляр (число)  есть вектор  такой, что , причем направление  совпадает с направлением , если  и противоположно ему, если .

4) Векторы и  коллинеарны, если .

5) Векторы  компланарны, если  (l, m — числа).

6) Скалярное произведение векторов и  есть скаляр , где . Векторы и  ортогональны, если .

Если  и , то .

7) Векторное произведение векторов и  есть вектор , где  и , причем  — правая тройка.  

Если , то

,

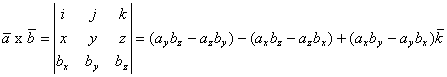где  — единичные векторы (орты), направленные по соответствующим осям координат (рис. 7.2).

8) Смешанное произведение.

=

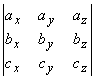
(геометрически ||=V параллелепипеда, построенного на векторах).

9) Длина и направление вектора  определяются:

где  — направляющие косинусы вектора .

10) Декартовы прямоугольные координаты точки M(x, y, z) пространства Oxyz есть , где  — радиус-вектор точки М (см. рис. 7.2),   и .