Понятие энтропии ввел Клаузиус в 1865 г. Энтропию можно ввести через приведенную теплоту. Приведенной теплотой называется отношение теплоты (Q), полученной телом в изотермическом процессе, к температуре (Т) тела: 
. Приведенное количество теплоты, сообщенное телу на бесконечно малом участке процесса, равно: 
. Теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу, в любом обратимом круговом процессе, равно нулю:
. (8.25)
Из равенства нулю интеграла (8.25) следует, что подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется лишь состоянием системы и не зависит от пути перехода в это состояние:
. (8.26)
Функция состояния (S) называется энтропией.
Из формулы (8.25) следует, что для обратимых процессов изменение энтропии равно нулю:
. (8.27)
В термодинамике доказывается, что для системы, совершающей необратимый цикл, энтропия возрастает:
. (8.28)
Объединяя формулы (8.27) и (8.28), можно записать, что изменение энтропии:
. (8.29)
Выражение (8.29) называется неравенством Клаузиуса. Сущность его в том, что энтропия замкнутой системы не убывает. Она может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
Изменение энтропии при переходе системы из состояния 1 в состояние 2 можно рассчитать, интегрируя выражение (8.26):
. (8.30)
Из первого начала термодинамики и выражения (8.29), можно получить:
. (8.31)
Можно рассчитывать изменение энтропии в различных процессах, применяя к ним интеграл (8.31). Расчеты дают следующие выражения для изменения энтропии:
а) в адиабатическом процессе
S = 0; (8.32)
б) в изотермическом процессе
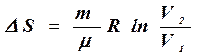, (8.33)
в) в изохорическом процессе
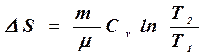, (8.34)
г) в изобарическом процессе
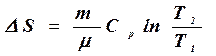. (8.35)
Из формул (8.32) – (8.35) видно, что изменение энтропии при переходе системы из состояния (1) в состояние (2) зависит только от параметров состояния и не зависит от процесса перехода 1
2.
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему.
Физический смысл энтропии заключается в том, что энтропия есть мера обесцененности энергии, то есть энтропия характеризует связанную энергию, которая в принципе не может превратиться в работу.
Более глубоко смысл энтропии вскрывается в статистической физике. Энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность (W) системы есть число способов, которыми может быть реализовано данное макроскопическое состояние системы, или это число микросостояний, которыми может быть реализовано данное макросостояние. По определению термодинамическая вероятность: W >1.
Согласно Больцману энтропия системы (S) и термодинамическая вероятность (W) связаны соотношением:
. (8.36)
Здесь k = 1,38 · 10-23 Дж/К – постоянная Больцмана, lnW – натуральный логарифм термодинамической вероятности. Использование lnW вместо самой вероятности (W) связано с аддитивностью этой величины:
если W = W1 W 2 ·W3, то lnW = lnW1 + lnW2 + lnW3 + …, что соответствует аддитивности энтропий: S = S1 + S2 + S3 + … .
Формула Больцмана (8.36) позволяет дать энтропии статистическое толкование: энтропия есть мера неупорядоченности системы. Другими словами, энтропия является мерой молекулярного беспорядка. В замкнутой системе процессы идут в направлении увеличения числа микросостояний, то есть в направлении увеличения термодинамической вероятности состояния, а следовательно, к возрастанию энтропии. Наиболее вероятным состоянием системы является равновесное состояние. Можно сказать, что в замкнутой системе все процессы идут от менее вероятных состояний к более вероятным, пока состояние не станет равновесным, а его вероятность максимальной. Этому состоянию отвечает максимальная энтропия (Smax). Эти утверждения могут нарушаться в системах с малым числом частиц. На определенном отрезке времени энтропия здесь может убывать, а не возрастать или оставаться постоянной.