Линейная зависимость – наиболее часто используемая форма связи между двумя коррелируемыми признаками и выражается при парной корреляции уравнением прямой:

.

Гипотеза именно о линейной зависимости между х и у выдвигается в том случае, если результативный и факторный признаки возрастают (или убывают) одинаково, примерно в арифметической прогрессии.

Параметры а₀ и а₁ отыскиваются, решив систему нормальных уравнений МНК для линейного уравнения регрессии:

.

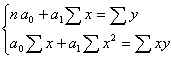Для решения этой системы применяется способ определителей 2-го порядка:

;

.

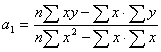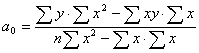Параметр а₁, т.е. коэффициент при х в уравнении линейной регрессии, называется коэффициентом регрессии. Он показывает, насколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу.

Рассмотрим расчет параметров уравнения регрессии между стоимостью основных фондов х и валовым выпуском продукции у.

Исходные данные и расчет необходимых сумм показан в табл. 8.1.

Таблица 8.1

Расчетная  таблица для определения параметров уравнения регрессии

Предположим, что зависимость между х и у линейная, т.е. .

Параметры а₀ и а₁ этого уравнения найдем, решив систему нормальных уравнений, подставив в нее необходимые суммы, рассчитанные в табл. 8.1.

Получаем:

.

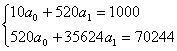Определяем значение а₁ и а₀ по формулам:

,

отсюда искомое уравнение регрессии у по х будет:

.

Коэффициент регрессии а₁ = 2,12, он показывает, что при увеличении стоимости основных фондов предприятий на 1 млн. р., валовой выпуск продукции увеличится на 2,12 млн. р.

Прежде чем проводить дальнейший анализ, необходимо оценить точность уравнения регрессии. Для этого вычисляются значения t – критерия Стьюдента.

Для проверки типичности параметров уравнения регрессии рассчитывается фактическое значение t – критерия по формулам:

для параметра а₀    ;

для параметра а₁    .

Остаточная дисперсия   исчисляется по формуле

,

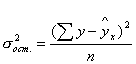где  — выровненные значения у_х.

.

Значения фактических и сравниваются с критическим t_к, который получают по таблицам Стьюдента с учетом принятого уровня значимости  и ,

;

где п – число наблюдений,

       к – число параметров уравнения.

Если , то вычисленные параметры уравнения признаются типичными.