Разработка мероприятий по снижению производственных вибраций должна производиться одновременно с решением основной задачи современного машиностроения: комплексной механизации и автоматизации производства. Введение дистанционного управления цехами и участками позволит полностью решить проблему защиты от вибраций.

В неавтоматизированных производствах осуществляют следующие методы по уменьшению вибрации:

· в источнике возникновения,

· на путях распространения,

· путем соответствующей организации труда,

· применения средств индивидуальной защиты и лечебно-профилактических мероприятий.

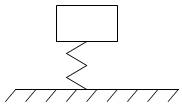
Рис. 8.3 Схема колебательной системы

Методы борьбы с вибрацией базируются на анализе уравнений, описывающих колебания машин и агрегатов в условиях производства. Эти уравнения сложны, так как любой вид технологического оборудования, так же как и его отдельные конструктивные элементы, является системой со многими степенями подвижности и обладает рядом резонансных частот.

Прежде всего, следует снижать вибрацию вблизи резонансов. В этом случае задача упрощается, так как машины и агрегаты можно рассматривать как колебательные системы с одной степенью свободы. При определении основных направлений борьбы с вибрацией следует ограничиться анализом уравнений вынужденных колебаний такой системы, которую можно представить в виде массы, покоящейся на пружине, другой конец ее жестко закреплен (рис. 8.3). Система, кроме

того, обладает трением. В этой системе с сосредоточенными параметрами элементы упругости, массы и трении отделены друг от друга. Для простоты анализа будем считать, что на систему воздействует переменная возмущающая сила, изменяющаяся по синусоидальному закону. Уравнение колебаний в этом случае имеет вид:

m +  + q x = F_m е ^jwt,

где m – масса системы, кг;  – текущее значение виброскорости (равное dx/dt) м/с;  – коэффициент сопротивления, (Н с)/м;  – текущее значение виброускорения массы (d² x / dt²), м²/с; q – коэффициент жесткости системы, Н/м; х – текущее значение вибросмещения; F_m – амплитуда вынуждающей силы, Н; w – угловая частота вынуждающей силы, рад/с.

Выражая вибросмещение в комплексном виде

x = А_m е ^jwt

и подставив соответствующие значения  и  в формулу, найдем выражение для соотношения между амплитудами виброскорости и вынуждающей силы:

V_{m =.}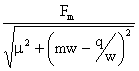

Знаменатель полученного выражения

z =

характеризует сопротивление, которое оказывает система вынуждающей переменной силе. Эта характеристика называется полным механическим импедансом колебательной системы.

Величина  составляет активную, а величина  – реактивную часть этого сопротивления. Реактивная часть, в свою очередь, состоит из двух сопротивлений: упругого  и инерционного . Механическое сопротивление измеряется в ньютонах, умноженных на секунду и деленных на метр (Н с/м).

Реактивное сопротивление равно нулю при резонансе, которому соответствует частота:

w = w₀ = .

При этом система оказывает сопротивление вынуждающей силе только за счет наличия активных потерь в системе. Амплитуда колебаний на таком режиме резко увеличивается. Амплитуду виброскорости при резонансе определяют по формуле:

V_{рез = ,}

где  – коэффициент потерь, характеризующий диссипативные силы в колебательной системе и определяющий значение амплитуды виброскорости при резонансе, .

При частотах ниже резонансной

mw <q/w,

т.е. в случае, когда инерционное сопротивление значительно меньше упругого, полное сопротивление системы возмущающей силе при небольшом трении практически оказывается равным упругому z = q/w. Следовательно, на этих частотах система оказывает упругое сопротивление, как при действии статической силы. Амплитуда вибросмещения при этом равна упругой деформации при статическом действии силы:

x_ст = F_m /q,

а амплитуда виброскорости

V_m= wF_m / q.

Если частота вынуждающей силы значительно выше резонансной, то mw>q/w. При малом трении  < mw, система будет оказывать только инерционное сопротивление z = mw. При этом амплитуда виброскорости будет равна:

V_m=.

С увеличением частоты (w) сопротивление системы (z) возрастает и виброскорость снижается. Система как бы стремится к неподвижности. Систему с инерционным сопротивлением широко используют при защите от вибраций.

Таким образом, из проведенного анализа решения уравнения вынужденных колебаний системы с одной степенью свободы следует, что основными методами борьбы с вибрациями машин и оборудования являются:

1) снижение вибраций воздействием на источник возбуждения (посредством снижения или ликвидации вынуждающих сил);

2) отстройка от режима резонанса путем рационального выбора массы или жесткости колеблющейся системы;

3) вибродемпфирование – увеличение механического импеданса колеблющихся конструктивных элементов путем увеличения диссипативных сил при колебаниях с частотами, близкими к резонансным;

4) динамическое гашение колебаний – присоединение к защищаемому объекту системы, реакции которой уменьшают размах вибрации объекта в точках присоединения системы;

5) изменение конструктивных элементов машин и строительных конструкций.

Методы вибрационной защиты могут быть также разделены на методы, снижающие параметры вибраций воздействием на источник возбуждения, и методы, снижающие параметры вибраций на путях ее распространения от источника. К последним относятся методы 2, 3, 4 приведенной классификации, а также виброизоляция и применение средств индивидуальной защиты.