1) Расстояние между двумя точками
и 
.
.
2) Уравнение плоскости с нормальным вектором 
, проходящей через точку 
, есть 
, где 
- радиус-вектор текущей точки 
, 
– радиус-вектор точки M0 .
В координатной форме эта плоскость имеет уравнение:
,
или
Ах + Ву + Сz + D =0, (*)
где 
.
3) Расстояние точки от плоскости (*) равно:
.
4) Векторное уравнение прямой линии в пространстве: 
, где 
— текущий радиус-вектор точки прямой, 
— направляющий вектор прямой.
В координатной форме уравнение прямой имеет вид:
— (канонические уравнения).
5) Прямая линия как пересечение плоскостей задается системой уравнений:
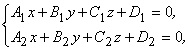
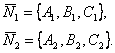
Направляющий вектор 
(рис. 8.1).
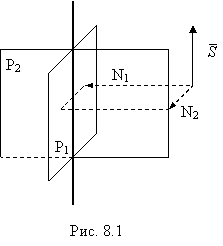
6) Уравнения прямой в параметрической форме:
x = x0 + mt, y = y0 + nt, z = z0 + kt, 
.
7) Уравнение плоскости, проходящей через три точки:
, , 
.
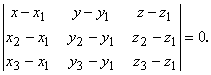
Пример 18. Записать уравнение плоскости, отсекающей по осям координат соответственно отрезки а, b и с.
Решение: используем уравнение плоскости, проходящей через три точки М1(a,0,0), M2(0,b,0) и М(0,0,с):
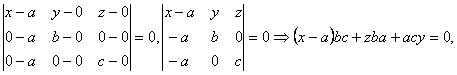
т.е. 
— уравнение плоскости в отрезках.
Пример 19. Записать уравнение плоскости, проходящей через точку М0(2;-3;1) и имеющей нормальный вектор 
Решение: Запишем уравнение плоскости, проходящей через данную точку М0 и перпендикулярной данному вектору:
или 4х + 3у — 5z + 6 = 0.
Пример 20. Найти величину отрезков, отсекаемых на осях координатной плоскостью 3х — 4у + 12z – 60 = 0.
Решение: приведём уравнение данной плоскости к уравнению в отрезках:
3х -4у + 12z =60.
.
Ответ: а = 20, b = -15, с = 5.
Пример 21. Записать уравнение прямой
и определить направляющие косинусы.
Решение: Имеем 
, следовательно, направляющий вектор
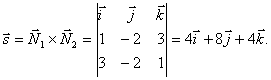
Найдём 
, следовательно:
Пример 22. Записать уравнения прямой, проходящей через две несовпадающие точки
М1(x1; y1; z1) и М2(x2; y2; z2).
Решение: За направляющий вектор прямой можно принять
,
тогда уравнение искомой прямой будет:
.
Пример 23. Записать уравнение прямой, проходящей через точку М0(3;-2;6) и параллельной оси Oz.
Решение: Поскольку прямая параллельна оси Oz, то 
и 
По каноническому уравнению получаем:
,
которые равносильны уравнениям:
,
Следовательно, искомая прямая перпендикулярна осям Ох и Оу.
Пример 24. Записать параметрические и канонические уравнения прямой, проходящей через точку М0(5;-10;6) параллельно вектору 
Решение: так как 
, то канонические уравнения прямой будут:
,
приравняв каждое из отношений параметру 
найдём параметрические уравнения:
8) Угол между плоскостями:
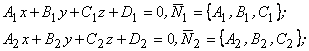
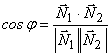или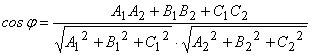 
,
где 
— двугранный угол между плоскостями.
9) Условия параллельности и перпендикулярности плоскостей:
||
;
10) Угол между двумя прямыми в пространстве
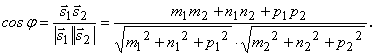
11) Условия параллельности и перпендикулярности прямых:
12) Угол между прямой и плоскостью
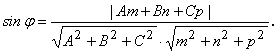
13) Взаимное расположение прямой и плоскости:
а) прямая и плоскость пересекаются, если Am + Bn + ≠ 0;
б) перпендикулярны, если 
,
в) параллельны, если 
, (
);
г) совпадают, если , 
.
Пример 25: Найти угол между плоскостями 2x-3y-2z+5=0 и 3x-5y+z-3=0.
Решение: Косинус угла (
);
Пример 26: Найти угол между прямой x = -2 — t, y = 3 — t, z = -3 + 2t и плоскостью 4x — 8y + 4z – 18 = 0.
Решение: Имеем 
, найдем
Откуда 
.
Пример 27. Найти проекцию точки M(2;-1;3) на плоскость 3x — 2y + 4z + 15 = 0.
Решение: Проекция точки на плоскость есть основание перпендикуляра, опущенного из данной точки на плоскость 3x-2y+4z+15=. Если провести прямую через этот перпендикуляр, то направляющим вектором этой прямой будет вектор 
, так как он совпадает с нормальным вектором данной плоскости. Следовательно, прямая, проходящая через точку M(2,-1,3) будет:
x = 2 + 3t, y = -1 — 2t, z = 3 + 4t.
Подставим эти выражения в уравнения плоскости, будем иметь:
3(2+3t)-2(-1-2t)+4(3+4t)+15=0, 29t=-35, t=35/29.
При этом значении t из уравнения прямой получаем:
.
Следовательно, точка M*(
) – искомая проекция.
Поверхности второго порядка
1) Цилиндрические поверхности:
а) с образующими параллельными оси OZ: F(x,y) = 0;
б) с образующими параллельными оси OX: F(y,z) = 0;
в) с образующими параллельными оси OY: F(x,z) = 0.
Пример 28: Указать, какие поверхности заданы уравнениями:
а) 
;
б) 
;
в) 
;
г) 
.
Решения:
а) в уравнении отсутствует явно переменная z, следовательно, имеем цилиндрическую поверхность с образующими параллельными оси OZ, направляющей служит окружность x2 + y2 = 4 (рис. 8.2, а) – прямой круговой цилиндр;
б) y = x2 – параболический цилиндр, с образующими параллельными оси OZ, y = x2 — направляющая (рис. 8.2, б);
в) x2 / 9 + z2 / 4 = 1 – эллиптический цилиндр, так как направляющая есть эллипс; образующие параллельные оси OY (рис. 8.2, в);
г) x2 - y2 = 4 – гиперболический цилиндр с образующими, параллельными оси OZ (рис. 8.2, г).
2) Поверхности вращения:
а) поверхность, образованная вращением линии l, x = x(z), y = y(z) вокруг оси OZ, задается уравнением x2 + y2 = x2(z) + y2(z);
б) поверхность, образованная вращением линии x = x1(у), z = z1(у) вокруг оси ОУ, задается уравнением 
;
в) поверхность, образованная вращением линии y = y2(x), z = z2(x) вокруг оси ОХ, задается уравнением 
.
Пример 29: Записать уравнения поверхностей вращения, если:
а) линия z = y2 вращается вокруг оси OZ;
б) линия x = y вращается вокруг оси ОУ.
Решение: а) так как линия z = y2 вращается вокруг оси OZ, то каждая ее точка описывает окружность радиуса 
с центром на оси OZ. Следовательно, в уравнении линии надо заменить y на , получим 
— параболоид вращения с осью вращения OZ (рис. 8.2, е).
Поверхности второго порядка
1) Уравнение сферы радиуса R с центром в точке С(x0, y0, z0):
если x0 = y0 = z0 = 0, то уравнение имеет вид: 
2) Уравнение трехосного эллипсоида с полуосями a, b и с:
.
3) Уравнение однополосного гиперболоида:
.
4) Уравнение двухполосного гиперболоида:
.
5) Уравнение конуса второго порядка:
.
6) Эллиптический параболоид:
.
7) Гиперболический параболоид (“седло”):
.
8) 
— пара пересекающихся плоскостей.
9) 
— пара параллельных плоскостей.
10) Уравнение параболоида вращения вокруг оси OZ:
x2 + y2 = 2pz.
Замечание: Вид поверхностей, соответствующих приведенным уравнениям, легко получить методом “сечений”.
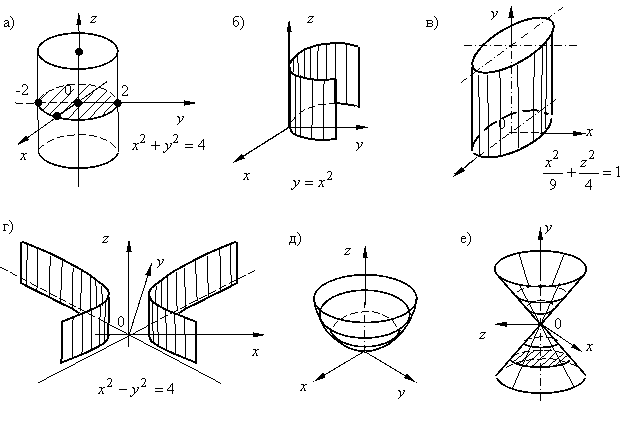
Рис. 8.2