Основным объектом исследования, как правило, является выборка экспериментальных данных, которая, чаще всего, представляется в виде массива, состоящего из пар чисел (x_i,y_i). В связи с этим возникает задача аппроксимации конкретной зависимости y(x_i) непрерывной функцией f(х). Функция f(х), в зависимости от специфики задачи, может отвечать различным требованиям:

- f(х) должна проходить через точки (x_i,y_i), т.е. f(x_i) = y_i, i = 1…n. В этом случае говорят об интерполяции данных функцией f(х) во внутренних точках между x_i или экстраполяции за пределами интервала, содержащего все х_i;

- f(х) должна некоторым образом (например, в виде определенной аналитической зависимости) приближать y(x_i), не обязательно проходя через точки (x_i,y_i).

Для построения интерполяции-экстраполяции в MathCAD имеется несколько встроенных функций, позволяющих "соединять" точки выборки данных (x_i,y_i) кривой разной степени гладкости. По определению интерполяция означает построение функции А(х), аппроксимирующей зависимость у(х) в промежуточных точках (между x_i). Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках x_i значения интерполяционной функции должны совпадать с исходными данными, т.е. A(x_i) = y (х_i).

Линейная интерполяция

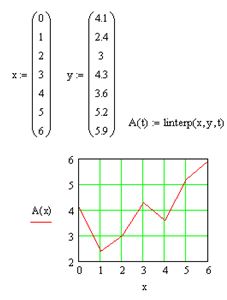
Рис. 8.1. Линейная интерполяция

Самый простой вид интерполяции – линейная, которая представляет искомую зависимость А(х) в виде ломаной линии. Интерполирующая функции А(х) состоит из отрезков прямых, соединяющих точки.

Для построения линейной интерполяции служит встроенная функция linterp (рис. 49) – функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью linterp (х, у, t), где  х – вектор действительных данных аргумента; у – вектор действительных данных значений того же размера; t – значение аргумента, при котором вычисляется интерполирующая функция.

Элементы вектора х должны быть определены в порядке возрастания, т.е. x₁<x₂<x_j<…<x_N.

Чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:

1) ввести векторы данных х и у (первые две строки листинга);

2) определить функцию linterp(x,y,t);

3) вычислить значения этой функции в требуемых точках, например:

linterp(x, y, 2.4) = 3.52;

linterp(х, у, 6) = 5.9,

или построить ее график.

Функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция A(t) вычисляется не только при значениях аргумента (т.е. в семи точках), а при го

раздо большем числе аргументов в интервале (0, 6), что автоматически обеспечивает MathCAD. Просто в данном случае эти различия незаметны, т.к. при обычном построении графика функции от векторного аргумента х MathCAD по умолчанию соединяет точки графика прямыми линиями (т.е. скрытым образом осуществляет их линейную интерполяцию), как показано на рис. 49.

Кубическая сплайн-интерполяция

В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т.е. отрезками кубических парабол interp(s, x, y, t) – функция, аппроксимирующая данные векторов х и у кубическими сплайнами:

s – вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;

х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у – вектор действительных данных значений того же размера;

t – значение аргумента, при котором вычисляется интерполирующая функция.

Сплайн-интерполяция в MathCAD реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определить первый из ее аргументов – векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х,у):

lspline(x, y) – вектор значений коэффициентов линейного сплайна;

pspline(х, у) – вектор значений коэффициентов квадратичного сплайна;

cspline (х, у) – вектор значений коэффициентов кубического сплайна:

х, у – векторы данных.

Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала.

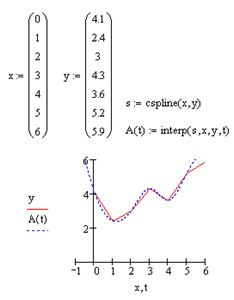
Рис. 8.2. Влияние

Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости

A(t) = at³ + bt² + ct + d.

Коэффициенты а, b, с, d рассчитываются независимо для каждого промежутка исходя из значений y_i в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения A(t) в любом точке t (рис. 50). Выбор вспомогательных функций cspline, pspline, lspiine существенно влияет на поведение А(t) вблизи граничных точек рассматриваемого интервала (0, 6) и особенно разительно меняет результат экстраполяции данных за его пределами.

Если на графике задать построение функции А(х) вместо A(t), то будет получено просто соединение исходных точек ломаной. Так происходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.

Полиномиальная сплайн-интерполяция

Более сложный тип интерполяции – так называемая интерполяция В-сплайнами (рис. 51). В отличие от обычной сплайн-интерполяции сшивка элементарных В-сплайнов производится не в точках x_i, а в других точках u_i, координаты которых предлагается ввести пользователю. Сплайны могут быть полиномами 1, 2 или 3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие со

стоит только в определении вспомогательной функции коэффициентов сплайна.

interp (s, х, у, t) – функция, аппроксимирующая данные векторов х с помощью В-сплайнов.

bspline(x, y, u, n) – вектор значений коэффициентов В-сплайна:

s – вектор вторых производных, созданный функцией bspiine;

х– вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у – вектор действительных данных значений того же размера;

t – значение аргумента, при котором вычисляется интерполирующая функция;

u – вектор значений аргумента, в которых производится сшивка В- сплайнов;

n – порядок полиномов сплайновой интерполяции (1, 2 или 3).

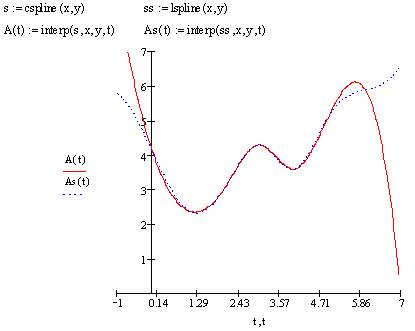
Рис. 8.3. Порядок

Размерность вектора u должна быть на 1, 2 или 3 меньше размерности векторов х и у. Первый элемент вектора и должен быть меньше или равен первому элементу вектора х, а последний элемент u – больше или равен последнему элементу х.

Сплайн-экстраполяция

Для вычисления экстраполяции достаточно просто указать соответствующее значение аргумента, которое лежит за границами рассматриваемого интервала. С

этой точки зрения разницы в применении в MathCAD между интерполяцией и экстраполяцией нет.

На практике при построении экстраполяции следует соблюдать известную осторожность, не забывая о том, что ее успех определяется значимостью ближайших к границе интервала точек.

Стандартные функции интерполяции-экстраполяции стоит применять только в непосредственной близости границ интервала данных. В MathCAD имеется более развитый инструмент экстраполяции, который учитывает распределение данных вдоль всего интервала. В функцию predict встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляции:

predict (у, m, n) – функция предсказания вектора, экстраполирующего выборку данных:

у – вектор значений, взятых через равные промежутки значений аргумента;

m – количество последовательных элементов вектора у, согласно которым строится экстраполяция;

n – количество элементов вектора предсказаний.

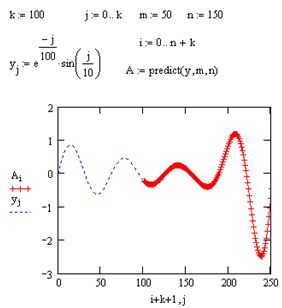
Рис. 8.4. Функция предсказания

Пример использования функции предсказания на примере экстраполяции осциллирующих данных y_j с меняющейся амплитудой приведен на рис. 52. Аргументы и принцип действия функции predict отличаются от рассмотренных выше встроен

ных функций интерполяции-экстраполяции. Значений аргумента для данных не требуется, поскольку по определению функция действует на данные, идущие друг за другом с равномерным шагом. Обратите внимание, что результат функции predict вставляется "в хвост" исходных данных.

Функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данных результат часто бывает неудовлетворительным. Кроме того, функция predict хорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью, в основном осциллирующего характера.

Линейная регрессия

Задачи математической регрессии имеют смысл приближения выборки данных (x_i, y_i) некоторой функцией f(x), определенным образом минимизирующей совокупность ошибок |f(х_i) – y_i|. Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость f(х). В силу производимого действия большинство задач регрессии являются частным случаем более общей проблемы сглаживания данных. Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных (x_i, y_i).

Самый простой и наиболее часто используемый вид регрессии – линейная. Приближение данных (x_i, y_i) осуществляется линейной функцией у(х) = b + а · х. На координатной плоскости (х, у) линейная функция, как известно, представляется прямой линией. Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и b вычисляются из условия минимизации суммы квадратов ошибок |b+ a·x_i  – y_i|.

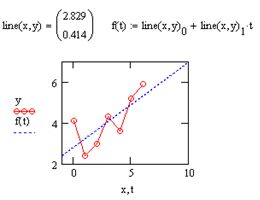
Рис. 8.5. Ломаная

Для расчета линейной регрессии в MathCAD имеется несколько способов. Выполняемые при этом действия дублируются, а результат получается одинаковым. Линейная регрессия по методу наименьших квадратов определяется функциями:

line(х, у) – вектор из двух элементов (b, а) коэффициентов линейной регрессии b + a · x (рис. 53);

intercept(х, у) – коэффициент b линейной регрессии;

slope(x,y) – коэффициент а линейной регрессии:

х – вектор действительных данных аргумента;

у – вектор действительных данных значений того же размера.

В MathCAD имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную регрессию для расчета коэффициентов а и b:

medfit(x, y) – вектор из двух элементов (b, а) коэффициентов линейном медиан-медианной регрессии b + а · х, где х, у – векторы действительных данных одинакового размера.

В MathCAD реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.

Полиномиальная регрессия

Полиномиальная регрессия означает приближение данных (x_i,y_i) полиномом k-й степени a(x) = a + bx+cx²+dx³+…+h·x^k при k = 1 полином является прямой линией, при k = 2 – параболой, при k = 3 – кубической параболой и т.д. Как правило, на практике применяются k < 5.

Для построения регрессии полиномом k-ой степени необходимо наличие, по крайней мере, (k + 1) точек данных.

В MathCAD полиномиальная регрессия осуществляется комбинацией встроенной функции reqress и полиномиальной интерполяции:

regress (x, у, к) – вектор коэффициентов для построения полиномиальной регрессии;

interp(s, x, y, t) – результат полиномиальной регрессии:

s = regress(x, y, k);

х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у – вектор действительных данных значений того же размера;

k – степень полинома регрессии (целое положительное число);

t – значение аргумента полинома регрессии.

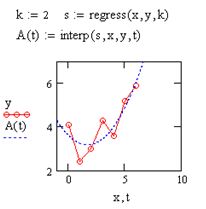
Рис. 8.6. Ломаная 2

Для построения полиномиальной регрессии после функции regress вы обязаны использовать функцию interp (рис. 8,6).

Помимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т.к. они имеют криволинейную форму) нескольких полиномов. Для этого имеется встроенная функция loess, применение которой аналогично функции regress:

loess (х, у, span) – вектор коэффициентов для построения регрессии данных отрезками полиномов;

interp(s, x, y, t) – результат полиномиальной регрессии:

s = loess(x, y, span);

х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у – вектор действительных данных значений того же размера;

span – параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span = 0,75).

Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (например, span=2 дает почти тот же результат, что и приближение точек параболой).

Регрессия одним полиномом эффективна, когда множество точек выглядит как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.