Требуется определить габаритные размеры цилиндрической косозубой двухпоточной передачи по данным примера (см. подразд. 7.4). Частота вращения шестерни  об/мин. Срок службы привода L_Г = 20 лет лет. Режим работы – постоянный. Коэффициент годового использования К_Г = 0,6. Коэффициент суточного использования К_с = 0,7. Привод – реверсивный.

Решение:

1. Срок службы привода

Определяем срок службы привода в часах по формуле:

;

ч.

2. Выбор материала зубчатых колес

В качестве материала зубчатых колес по табл. 9.2 выбираем сталь 40ХН, термообработка У+ТВЧ. Механические характеристики материала заносим в табл. 9.15.

Таблица 9.12 Механические характеристики сталей

Марка стали	Dпред, мм	Sпред, мм	Термообработка	Твердость заготовки
				поверхности	сердцевины
40ХН	200	125	У + ТВЧ	48…53 HRC	269…302 НВ

3. Расчет допускаемых контактных напряжений

Определяем предел контактной выносливости материала шестерни и колеса по формуле (см. табл. 9.3):

 МПа.

Для колес с поверхностным упрочнением зубьев (поверхностная закалка ТВЧ, цементация, азотирование) . Принимаем .

Для постоянного режима нагружения эквивалентное число циклов перемен напряжений материалов шестерни и колеса определяем по формуле:

;

;

.

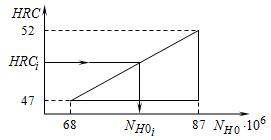
Рис. 9.14. К определению базового числа циклов  перемен напряжений

По табл. 9.4 в зависимости от средней твердости методом линейной интерполяции определяем базовое число циклов перемен напряжений материалов шестерни и колеса. Из подобия треугольников (рис. 9.11) имеем:

;

;

.

Поскольку  и  <  коэффициенты долговечности принимаем равными .

Определяем допускаемое контактное напряжение:

;        Мпа.

4. Проектный расчет на контактную выносливость. Определение основных геометрических параметров передачи

По табл. 9.5 назначаем коэффициент ширины колеса по межосевому расстоянию:

.

По табл. 9.6 в зависимости от расположения колеса относительно опор предварительно выбираем коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца. По условию задачи оно несимметричное (см. рис. 7.5), поэтому выбираем:

.

Определяем по формуле 9.14 межосевое расстояние:

 мм.

Принимаем стандартное значение  мм (см. подразд. 9.8).

Определяем модуль зацепления по следующей рекомендации:

;

 мм

Из полученного интервала модулей выбираем стандартное значение (см. подразд. 9.8):

.

Определяем ширину зубчатого венца колеса:

;        мм.

Принимаем из ряда нормальных линейных размеров (ГОСТ 6636-69) ширину зубчатого венца колеса  мм.

Определяем минимальный угол наклона зубьев:

;

.

Определяем суммарное число зубьев:

;

.

Принимаем .

Уточняем угол наклона зубьев по формуле (9.8):

;    .

Определяем по формулам (9.10) число зубьев шестерни и колеса:

;        .

Уточняем передаточное число:

;      ;;

;    .

Определяем по формулам (9.6) делительные диаметры:

 мм;        мм.

По формуле (9.1) проверяем межосевое расстояние:

.

Определяем диаметры вершин и впадин зубьев:

;    ;

;     мм;

;     мм.

5. Проверочный расчет на контактную выносливость

Поверочный расчет на контактную выносливость проводим по формуле (9.15)

.

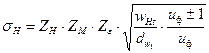Коэффициент  при суммарном коэффициенте смещения . При изготовлении зубчатых колес из сталей коэффициент  МПа^1/2.

Для косозубой цилиндрической передачи при коэффициенте осевого перекрытия  коэффициент  определяем по формуле:

.

Для цилиндрических передач, изготовленных без смещения, коэффициент торцевого перекрытия определяем по формуле:

;

;

.

Удельную окружную силу  определяется по формуле:

.

Определяем окружное усилие:

;        .

Значение коэффициента  определяем по табл. 9.7 в зависимости от степени точности передачи. Степень точности назначаем по табл. 9.8 в зависимости от окружной скорости:

;      м/с,

следовательно, степень точности – 9; .

Значение коэффициента  определяем по табл. 9.6 в зависимости от значения коэффициента ширины зубчатого венца:

;       ;          .

Значение коэффициента  назначаем по табл. 9.9;

;

.

6. Определение допускаемых напряжений изгиба

Допускаемые напряжения изгиба при расчете на выносливость определяем отдельно для колеса и шестерни по формуле (9.13)

.

При поверхностной закалке (40…56 HRC) предел выносливости , коэффициент безопасности  (см. табл. 9.3).

Для реверсивных передач при твердости НВ > 350 коэффициент .

Для поверхностно закаленных и азотированных сталей коэффициент, учитывающий размеры зубчатых колес, равен:

;          .

При полировании коэффициент, учитывающий шероховатость переходной поверхности зубьев, равен   (большие значения при улучшении и закалке ТВЧ).  Принимаем .

Коэффициент долговечности по напряжениям изгиба определяем по формуле:

.

Здесь при НВ > 350 показатель степени кривой усталости , ;  – базовое число циклов перемен напряжений для всех сталей;  – эквивалентное число циклов перемен напряжений, которое определяется аналогично определению числа циклов .

Определяем эквивалентное число циклов перемен напряжений:

;

.

Поскольку  и  коэффициенты долговечности принимаем равными .

Определяем допускаемые напряжения изгиба:

 МПа.

7. Проверочный расчет на выносливость при изгибе

Расчетные напряжения изгиба на переходной поверхности зубьев шестерни и колеса определяются по формуле:

.

Коэффициент формы зуба () определяем (см. рис. 9.12) в зависимости от эквивалентного числа зубьев шестерни () и колеса () (см. подразд. 9.12) и коэффициентов смещений  и .

Эквивалентные числа зубьев шестерни и колеса определяем по формуле:

;       ;       .

Находим по рис. 9.11 при коэффициентах смещения шестерни и колеса  значения коэффициентов формы зуба:

;       .

Коэффициент, учитывающий угол наклона зубьев, определяем по формуле:

.

Коэффициент осевого перекрытия определяем по формуле:

;              ;

.

Коэффициент, учитывающий перекрытие работы зубьев, равен:

;               .

Удельную окружную силу  определяем по формуле:

.

На основании результатов экспериментальных исследований передач с углом наклона зубьев  значение коэффициента  можно определить по формуле [3]:

,

где  – коэффициент высоты головки зуба (см. подразд. 9.1). Таким образом,

.

Значение коэффициента  можно также принять равным значению коэффициента  (см. табл. 9.7).

Значения коэффициентов определяем по табл. 9.10 и 9.11. Для симметричного расположения колеса относительно опор при HB > 350 .

Таким образом, удельная окружная сила равна:

.

Проверяем прочность зубьев шестерни и колеса по напряжениям изгиба:

;

.