1) Основные теоремы о пределах:
а) ![]()
б) 
в)  если lim f2(х) ≠ 0.
если lim f2(х) ≠ 0.
2) Замечательные пределы:
а) ![]()
б) ![]()
в) ![]()
г) 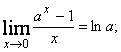
д) 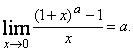
3) Эквивалентные бесконечно малые:
![]()
называются эквивалентными, если 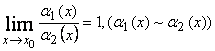 .
.
Замечание: для раскрытия неопределенностей вида 0/0 часто бывает полезным понятие эквивалентных бесконечно малых. Имеется принцип замены бесконечно малых: при раскрытии неопределенностей вида 0/0 можно и числитель, и знаменатель этой неопределенности заменить величинами, им эквивалентными.
Пример 30: Найти:
а) 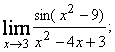 б)
б)  ;
;
в) 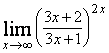 г)
г) ![]() ,
,
д) ![]() е)
е) 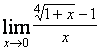
ж) 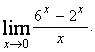
Решение:
а) ![]() ~ х2 — 9 при
~ х2 — 9 при ![]() , тогда
, тогда
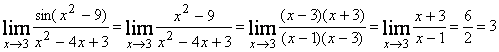 ;
;
б)  ;
;
в) 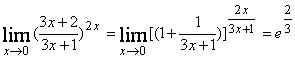 ;
;
г) 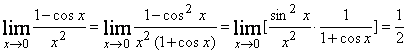 ;
;
д) ![]() ;
;
е)  ;
;
ж) 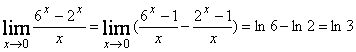 .
.
4) Связь между десятичным и натуральным логарифмом:
lg x = Mlnx, M = lge = 0,4342…
5) Приращение функции y = f(x), соответствующее приращение ![]() аргумента x:
аргумента x:
![]()
6) Условие непрерывности функции y = f(x):
![]() .
.
Если существуют конечные ![]() и
и ![]() не все три числа
не все три числа ![]() равны между собой, то x0 называется точкой разрыва первого рода; если есть бесконечность, то второго рода.
равны между собой, то x0 называется точкой разрыва первого рода; если есть бесконечность, то второго рода.
7) Производная
![]()
Геометрически ![]() - угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой x0.
- угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой x0.
8) Правила нахождения производных и сводка формул для производных:
8.1) ![]() .
.
8.2) ![]() .
.
8.3) ![]() .
.
8.4) ![]() .
.
8.5) ![]() .
.
8.6) ![]() .
.
8.7)  .
.
8.8) ![]() .
.
8.9) ![]() .
.
8.10) ![]() .
.
8.11) 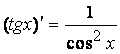 .
.
8.12) 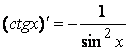 .
.
8.13) ![]() .
.
8.14) ![]() .
.
8.15) ![]() .
.
8.16) ![]() .
.
8.17)  .
.
8.18) 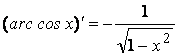 .
.
8.19) ![]() .
.
8.20) ![]() .
.
8.21) ![]() .
.
8.22) ![]() .
.
8.23) ![]() то
то 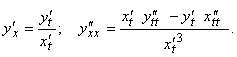
Пример 31. Исследовать функции на непрерывность:
а) ![]() ;
;
б) ![]()
в) ![]()
Решение:
а) Найдем![]() =(
=(![]() )
)![]() ;
; ![]() следовательно, функция
следовательно, функция ![]() — непрерывна.
— непрерывна.
б) функция ![]() определена для
определена для ![]() , непрерывна на всей числовой оси, так как
, непрерывна на всей числовой оси, так как ![]() .
.
 в) функция
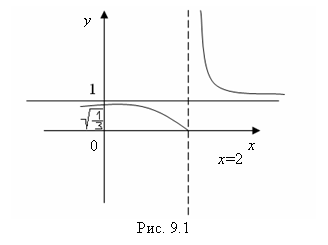
в) функция ![]() определена везде, кроме x=2. Найдем:
определена везде, кроме x=2. Найдем:

Следовательно, точка x0 = 2 есть точка разрыва второго рода. Когда![]() , то
, то ![]() , т.е. у = 1 — асимптота графика кривой
, т.е. у = 1 — асимптота графика кривой ![]() ,
,  — точка пересечения графика с осью ординат (рис. 9.1).
— точка пересечения графика с осью ординат (рис. 9.1).
Пример 32: Найти производные следующих функций:
а) y = cos 5x,
б) ![]() ,
,
в) ![]() ,
,
г) ![]()
Решение:
а) используем формулу для производной сложной функции ![]() , где
, где ![]() ,
, ![]() ,
, ![]()
![]() Следовательно,
Следовательно, ![]() ;
;
б) аналогично: ![]() , тогда
, тогда ![]() ,
,
![]() ;
;
в) имеем ![]() тогда
тогда ![]() ;
;
г) ![]() , то есть
, то есть ![]() поэтому
поэтому
![]() .
.
Примеры 33: Найти производные от дифференциальных функций, заданных неявно и параметрически:
а) x2 + y2 – xy = 1;
б) x3 + y3 – xy = 0;
в) y = x + ln y;
г) x = accost, y = b sin t;
д) x = wt, y = teat.
Решение:
а) Производная от неявной функции находится по правилу: дифференцируют функцию как тождество, считая y = y(x), то есть сложной функцией от x:
![]() .
.
Откуда ![]() - есть производная неявной функции;
- есть производная неявной функции;
б) по аналогии: ![]() , откуда
, откуда
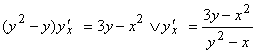 ;
;
в) 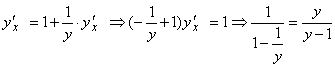 .
.
Замечание: если требуется найти y¢x в некоторой точке M0(x0, y0), то это выполняется привычным образом, только следует иметь в виду, что данная функция должна быть определена в рассматриваемой точке M0. Так, для примера в) зададим точку M0(1, 1). Проверим, удовлетворяют ли координаты x = 1, y = 1 уравнению y = x + ln y: 1 = 1 + ln 1, 1 = 1. Следовательно, 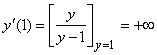 - производная в данной точке не существует.
- производная в данной точке не существует.
г) По формуле ![]() найдем сначала y¢t = b cos t, xt’ = -a sin t; подставив в формулу, получим:
найдем сначала y¢t = b cos t, xt’ = -a sin t; подставив в формулу, получим: ![]()
д) ![]() и
и ![]()
Для данного примера найдем ![]() . Для чего необходимо найти:
. Для чего необходимо найти:
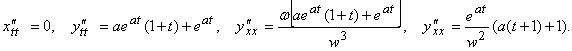 9) Правило Лопиталя для неопределенностей
9) Правило Лопиталя для неопределенностей ![]() и
и ![]() :
:
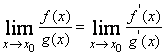 ,
,
если предел справа существует.
Примеры 34: Используя правило Лопиталя, найти следующие пределы:
а) ![]() ; б)
; б) 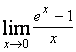 ;
;
в) 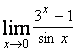 ; г)
; г) 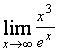 ;
;
д) ![]() ; е)
; е)  .
.
Решения:
а)  ;
;
б) 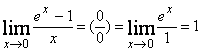 ;
;
в) 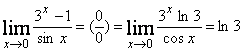 ;
;
г) 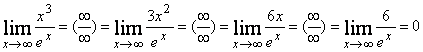 ;
;
д) ![]()
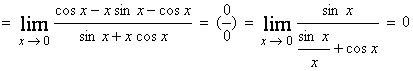 ;
;
е) для функции f(x)= ![]() могут быть получены неопределенности вида
могут быть получены неопределенности вида ![]() . В этом случае целесообразно логарифмировать функцию f(x). Обозначим наш предел буквой A, то есть:
. В этом случае целесообразно логарифмировать функцию f(x). Обозначим наш предел буквой A, то есть:
 .
.
Логарифмируем, получим (учтя непрерывность логарифмической функции):

Отсюда A = e0 = 1.
10) Теорема Лагранжа о конечном приращении дифференцируемой функции
f (b) – f (a) = f ¢(c) (b — a),
где ![]() .
.
11) Функция y = f (x) возрастает, если f ¢(x) > 0, и убывает, если f ¢ (x) < 0.
12) Формула Тейлора
![]()
где ![]() существует в окрестности точки x0. При x0 = 0 имеем
существует в окрестности точки x0. При x0 = 0 имеем
![]() — формулу Маклорена.
— формулу Маклорена.
Отметим, что наиболее употребительной формулой для остаточного члена формулы Тейлора является так называемая форма Лагранжа этой формулы:
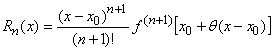 .
.
Если x0 = 0, то формула принимает вид
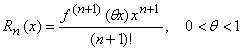 .
.
Пример 35: Записать формулу Маклорена для функции f(x) = ex и оценить погрешность при n = 8.
Решение: Формула Маклорена для функции f(x) = ex имеет вид:
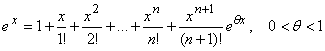 ,
,
где положено f(0) = 1, f¢‘(0) = 1, … f (n)(0) = 1, f (n+1)(x) = ex.
Если в формуле отбросить остаточный член, то получим приближенную формулу
![]() .
.
Поскольку![]() , то для x>0 погрешность оценивается неравенством
, то для x>0 погрешность оценивается неравенством
 .
.
Так, при x = 1 получаем
![]() .
.
Дадим, например, n=8 и проведем вычисления, с пятью десятичными знаками, тогда получим e=2.71827. Здесь верны первые четыре знака, так как ошибка не превосходит ![]() или 0,00001.
или 0,00001.
13) Необходимое условие экстремума f(x) в точке x0:
f¢¢ (x0) = 0 или f ¢(x0) не существует.
14) Достаточные условия экстремума f(x) в точке x0:
а) f¢‘(x0) = 0, f¢‘(x0 - 0) f¢‘(x0 + 0) < 0;
б) f¢‘(x0) = 0, f² ‘(x0) ¹ 0.
15) График функции y = f(x) вогнут вверх, если f² ‘(x0) > 0, и вогнут вниз, если f² (x0) < 0.
16) Необходимое условие точки перегиба графика функции y = f(x) при x = x0: f² (x0) = 0, f²‘(x0) не существует.
17) Достаточное условие точки перегиба при x = x0:
![]() .
.
18) Если f(x) непрерывна на [a,b] и f(a)f(b) < 0, то корень C уравнения f(x) = 0 приближенно может быть найден по формулам:
а) ![]() (метод хорд);
(метод хорд);
б) ![]() , где
, где ![]() (метод касательных).
(метод касательных).
19) Дифференциал независимой переменной х: ![]()
Дифференциал функции y = f(x):![]() . Связь приращения
. Связь приращения ![]() функции с дифференциалом dy функции:
функции с дифференциалом dy функции:
![]() , где
, где ![]() при
при ![]() .
.
20) Приближенное вычисление значения функции с помощью дифференциала, можно проводить по формуле:
![]()
21) Дифференциал второго порядка функции y = f(x), где х – независимая переменная (d2x = 0):
![]() .
.
Пример 36: Найти точки перегиба графика функции ![]() .
.
Решение: Найдем ![]() . Приравняв нулю
. Приравняв нулю ![]() , найдем критическую точку:
, найдем критическую точку:
![]() .
.
Используем достаточное условие точки перегиба:
![]() , то есть
, то есть ![]() ,
,
так как ![]() .
.
Следовательно, при ![]() функция
функция ![]() имеет перегиб и
имеет перегиб и ![]() .
.
Пример 37: Вычислить приближенное значение выражения ![]() с помощью дифференциала.
с помощью дифференциала.
Решение: Используя формулу ![]() , положим
, положим ![]() а
а ![]() , тогда
, тогда ![]()
![]() и
и ![]() .
.
Ответ: ![]() .
.
Пример 38: Найти приращение функции y = x3 на отрезке ![]() и проверить теорему Лагранжа.
и проверить теорему Лагранжа.
Решение: Приращение функции ![]() будет
будет
![]() , так как
, так как ![]() .
.
Формула Лагранжа дает:
![]() ,
,
то есть ![]() .
.
Следовательно, теорема Лагранжа имеет место.
Пример 39: Найти ![]() и
и ![]() , если
, если ![]() .
.
Решение: Используя определение дифференциала функции, найдем ![]() и
и ![]()
![]() .
.
Следовательно, ![]() .
.
22) Уравнение касательной к кривой у = f (x) в точке М0(х0, у0):
![]() ,
, ![]() — угловой коэффициент касательной.
— угловой коэффициент касательной.
23) Уравнение нормали к кривой у = f (x) в точке М0:
![]() .
.
24) Механический смысл производной.
Если x = f(t) – закон прямолинейного движения точки, то ![]() — скорость движения в момент времени t.
— скорость движения в момент времени t.
25) Механический смысл дифференциала: пусть s = f(t) – закон прямолинейного движения точки, где s – длина пути, t – время, тогда![]() , где v(t) – скорость движения. Следовательно, дифференциал пути равен приращению пути, в предположении, что, начиная с данного момента t, точка движется равномерно, сохраняя приобретённую скорость.
, где v(t) – скорость движения. Следовательно, дифференциал пути равен приращению пути, в предположении, что, начиная с данного момента t, точка движется равномерно, сохраняя приобретённую скорость.
26) Механический смысл производной второго порядка: пусть x = f(t) – закон движения точки М по оси Ох; пусть в момент t точка М имеет скорость v(t), а в момент ![]() — скорость
— скорость![]() . Отношение
. Отношение ![]() (среднее ускорение движения), предел этого отношения при
(среднее ускорение движения), предел этого отношения при ![]() называется ускорением точки М в данный момент времени t, то есть
называется ускорением точки М в данный момент времени t, то есть
![]()
![]() .
.
27) Кривизна кривой у = f(х) в точке М0(х0, у0):
а) 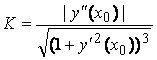 — когда линия задана в декартовых координатах;
— когда линия задана в декартовых координатах;
б) 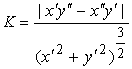 — когда линия задана параметрически;
— когда линия задана параметрически;
в) 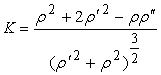 — когда линия задана в полярных координатах.
— когда линия задана в полярных координатах.
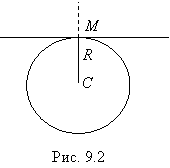
28) Радиус кривизны данной кривой в данной точке определяется по формуле
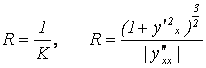
и откладывается по нормали к кривой в точке М в сторону вогнутости кривой (рис. 9.2). Точка С – центр кривизны кривой, а окружность радиуса R называется окружностью кривизны кривой в точке М.
 Пример 40. Записать уравнения касательной и нормали к кривой у = х2 в точке М0(2;4).
Пример 40. Записать уравнения касательной и нормали к кривой у = х2 в точке М0(2;4).
Решение: Найдём![]() ,
, ![]() ; тогда, используя уравнения касательной и нормали, получим:
; тогда, используя уравнения касательной и нормали, получим:
у – 4 = 4(х — 2), у = 4х + 2 – уравнение касательной;
![]() ,
, ![]() — уравнение нормали.
— уравнение нормали.
Пример 41. Найти кривизну синусоиды y = sin x в точке ![]() .
.
Решение: Используя формулу для кривизны кривой, заданной в декартовых координатах, найдём ![]() . Тогда кривизна кривой в произвольной точке будет
. Тогда кривизна кривой в произвольной точке будет
![]() .
.
При ![]() имеем
имеем ![]() , k = 0.
, k = 0.
Пример 42. С какой скоростью возрастает площадь круга в тот момент, когда радиус его R = 10 м, если радиус круга растёт со скоростью 2 м/с?
Решение: используем физический смысл дифференциала, зная, что площадь круга ![]() , найдём
, найдём ![]() .
.
Пример 43. Закон движения точки ![]() . Найти скорость и ускорение движения.
. Найти скорость и ускорение движения.
Решение: используя физический смысл скорости и ускорения движения точки, получаем:
V = 2 + 3t; a = 3.