1) Центроидный – был рассмотрен выше. В общем случае:

,

где – область определения.

Для дискретного варианта формула имеет вид:

.                                                          (4.1)

2) Первый максимум (First-of-Maxima). Четкая величина вывода находится как наименьшее значение, при котором достигается максимум итогового нечеткого множества (рис. 4.19):

.

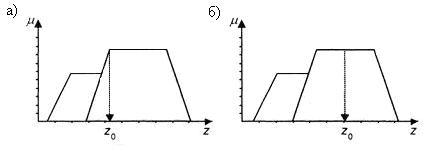
Рис. 4.19. Иллюстрация к методам приведения к четкости: а – первый максимум; б – средний максимум

3) Средний максимум (Middle-of-Maxima). Четкое значение для дискретного варианта находится по формуле

.

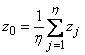4) Критерий максимума (Max-Criterion). Четкое значение выбирается произвольно среди множества элементов, для которых  достигает максимума:

.

5) Высотная дефаззификация (Height defuzzification). Элементы области определения , для которых значения функции принадлежности меньше, чем некоторый уровень , в расчет не принимаются, и четкое значение рассчитывается в соответствии с выражением

,

где – нечеткое множество -уровня. Для дискретного варианта формула имеет вид (4.1), где .