Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения m_A(x), на оси абсцисс в произвольном порядке расположены элементы E (мы уже использовали такое представление в примерах нечетких множеств). Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами (рис. 4.3).

На рис. 4.3, а заштрихованная часть соответствует нечеткому множеству A и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в A. На рис. 4.3, б, в, г даны , AÇ, AÈ.

           а)                                                б)

в)                                                г)

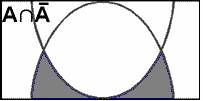
Рис. 4.3. Графическая интерпретация логических операций:

а – нечеткое множество A; б – нечеткое множество ;

в – AÇ; г – AÈ

Свойства операций È и Ç.

Пусть А, В, С – нечеткие множества, тогда выполняются следующие свойства:

· коммутативность;

·  ассоциативность;

·  идемпотентность;

·  дистрибутивность;

· AÈÆ = A, где Æ – пустое множество, т.е. " xÎE;

· AÇÆ = Æ;

· AÇE = A, где E – универсальное множество;

· AÈE = E;

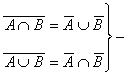·  теоремы де Моргана.

В отличие от четких множеств, для нечетких множеств в общем случае:

AÇ ¹ Æ,

AÈ ¹ E.

(Что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств).

Замечание. Введенные выше операции над нечеткими множествами основаны на использовании операций max и min. В теории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им связок "и", "или", "не".

Один из подходов к операторам пересечения и объединения заключается в их определении в классе треугольных норм и конорм.

Треугольной нормой (t-нормой) называется двуместная действительная функция T:[0,1]´[0,1]®[0,1], удовлетворяющая следующим условиям:

1) T (0,0)=0; T (m_A, 1) = m_A; T (1, m_A) = m_A – ограниченность;

2) T (m_A, m_B) £ T (m_C, m_D), если m_A£m_C , m_B£m_D – монотонность;

3) T (m_A , m_B) = T (m_B, m_A) – коммутативность;

4) T (m_A, T(m_B, m_C))= T( T(m_A, m_B), m_C) – ассоциативность.

Простым случаем треугольных норм являются:

min(m_A, m _B)

произведение m_A×m_B

max(0, m_A + m_B -1).

Треугольной конормой (t-конормой) называется двуместная действительная функция S:[0,1]´[0,1]® [0,1], со свойствами:

1) S (1,1) = 1; S (m_A,0) = m_A; S (0, m_A) = m_A – ограниченность;

2) S (m_A, m_B)³ S (m_C, m_D), если m_A ³m_C, m_B ³m_D – монотонность;

3) S (m_A, m_B) = S (m_B, m_A) – коммутативность;

4) S (m_A, S (m_B, m_C)) = S (S (m_A, m_B), m_C) – ассоциативность.

Примеры t-конорм:                      max(m_A, m_B)

m_A + m_B — m_A× m_B

min(1, m_A + m_B).