Когда нет необходимости, чтобы сеть в явном виде выдавала образец, то есть достаточно, скажем, получать номер образца, ассоциативную память успешно реализует сеть Хэмминга. Данная сеть характеризуется, по сравнению с сетью Хопфилда, меньшими затратами на память и объемом вычислений, что становится очевидным из ее структуры (рис. 2.20).

Сеть состоит из двух слоев. Первый и второй слои имеют по m нейронов, где m – число образцов. Нейроны первого слоя имеют по n синапсов, соединенных со входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой ингибиторными (отрицательными обратными) синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с его же аксоном.

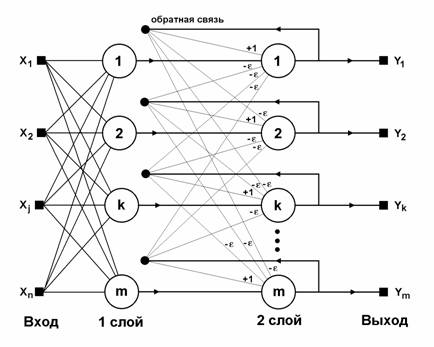
Рис. 2.20. Структурная схема сети Хэмминга

Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным рас

стоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.

На стадии инициализации весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:

, i = 1, …, n,            k = 1, …, m,                              (2.47)

T_k = n / 2, k = 1, …, m.                                              (2.48)

Здесь x_i^k – i-й элемент k-го образца.

Весовые коэффициенты тормозящих синапсов во втором слое берут равными некоторой величине 0 < e < 1/m. Синапс нейрона, связанный с его же аксоном, имеет вес +1.

Алгоритм функционирования сети Хэмминга следующий:

1) На входы сети подается неизвестный вектор x = {x_i: i=1, …, n}, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):

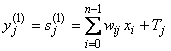, j=1, …, m.                                (2.49)

После этого полученными значениями инициализируются значения аксонов второго слоя:

y_j⁽²⁾ = y_j⁽¹⁾, j=1, …, m.                                             (2.50)

2) Вычислить новые состояния нейронов второго слоя:

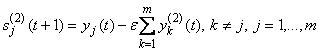                   (2.51)

и значения их аксонов:

                              (2.52)

Активационная функция f имеет вид порога (см. рис. 2.19, б), причем величина F должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.

3) Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – конец.

Из оценки алгоритма видно, что роль первого слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети (заменен на матрицу весовых коэффициентов), что и было сделано в ее конкретной реализации, описанной ниже.

Обсуждение сетей, реализующих ассоциативную память, было бы неполным без хотя бы краткого упоминания о двунаправленной ассоциативной памяти (ДАП). Она является логичным развитием парадигмы сети Хопфилда, к которой для этого достаточно добавить второй слой. Структура ДАП представлена на рис. 2.21. Сеть способна запоминать пары ассоциированных друг с другом образов. Пусть пары образов записываются в виде векторов x^k = {x_i^k: i = 1, …, n} и y^k = {y_j^k: j=1, …, m}, k=1, …, r, где r – число пар. Подача на вход первого слоя некоторого вектора u = {u_i: i=1, …, n} вызывает образование на входе второго слоя некоего другого вектора h = {h_j: j=1, …, m}, который затем снова поступает на вход первого слоя. При каждом таком цикле вектора на выходах обоих слоев приближаются к паре образцовых векторов, первый из которых – x – наиболее походит на u, который был подан на вход сети в самом начале, а второй – y –

ассоциирован с ним. Ассоциации между векторами кодируются в весовой матрице W⁽¹⁾ первого слоя. Весовая матрица второго слоя W⁽²⁾ равна транспонированной первой (W⁽¹⁾)^T. Процесс обучения, так же как и в случае сети Хопфилда, заключается в предварительном расчете элементов матрицы W (и соответственно W^T) по формуле

.                                   (2.53)

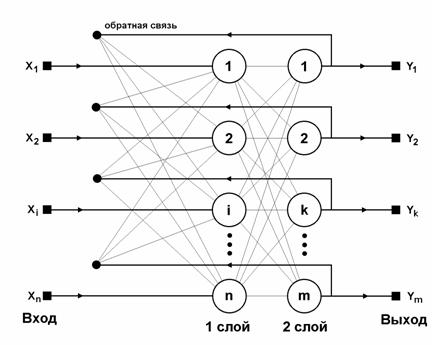
Рис. 2.21. Структурная схема ДАП

Эта формула является развернутой записью матричного уравнения

                                                       (2.54)

для частного случая, когда образы записаны в виде векторов, при этом произведение двух матриц размером соответственно [n*1] и [1*m] приводит к (2.53).

В заключение можно сделать следующее обобщение. Сети Хопфилда, Хэмминга и ДАП позволяют просто и эффективно разрешить задачу воссоздания образов по неполной и искаженной информации. Невысокая емкость сетей (число запоминаемых образов) объясняется тем, что сети не просто запоминают образы, а позволяют проводить их обобщение, например, с помощью сети Хэмминга возможна классификация по критерию максимального правдоподобия. Вместе с тем, легкость построения программных и аппаратных моделей делают эти сети привлекательными для многих применений.