Задача 4.1. В результате наблюдения в течение времени Т за производственной деятельностью подсистем ПС определены значения следующих параметров:

  и  

Ставится задача увеличить производительность ПС х₀ на С % по отношению к имеющейся при минимальных затратах на реорганизацию ПС.

Решение.  1. Находится новое значение производительности ПС:

2. Решается система балансовых уравнений (4.10) при заданном  и находятся новые значения производительности  подсистем ПС  сбалансированные с :

3. Определяются значения коэффициентов посещения r_k подсистем.

4. Строится ряд по убыванию из произведений r_kv_k:

                                    (4.12)

5. Если 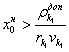, то делается заключение, что имеющейся мощности у модуля недостаточно для обеспечения производительности ПС, равной  Необходимо ее увеличить в раз, где

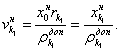
Далее аналогичным образом проверяется, надо ли увеличивать и во сколько раз мощность последующих в ряду (4.12) модулей  ПС.

Если 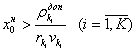, то делается заключение, что мощность модуля  и последующих за ним в ряду (4.12) модулей ПС достаточна для обеспечения производительности ПС, равной

Так как по изложенному методу увеличивается мощность только тех подсистем ПС, которые действительно препятствуют повышению производительности ПС на С %, то суммарная величина затрат на требуемую реконструкцию подсистем ПС будет предельно минимальной.

Задача 4.2. Требуется сбалансировать коэффициенты загрузки подсистем ПС при условии, что производительность самой системы х₀ не должна измениться.

Решение. Решение поставленной задачи будет достигнуто, если у каждой k-й  подсистемы ПС коэффициент загрузки   будет равен , где   — максимально допустимое значение коэффициента загрузки k-й подсистемы. Если, на

пример, необходимое резервирование мощности k-й подсистемы не должно быть меньше 15 %, то = 0,85. На практике часто принимают

Увеличение коэффициента загрузки каждой k-й подсистемы ПС может быть достигнуто только в результате увеличения средней продолжительности выполнения одной работы v_k (что идентично уменьшению мощности модуля R_k ПС): значения интенсивностей изменять нельзя, так как при  изменении значений х_k,  может измениться производительность ПС х₀.

Пусть  есть скорректированное значение , равное . Тогда имеем

откуда следует, что скорректированное значение средней продолжительности выполнения каждой работы в R_k ПС будет равно

Таким образом, за счет увеличения у каждой подсистемы R_k ПС значения параметра v_k до  т.е. на величину

мощности всех подсистем ПС будут взаимно сбалансированы.

Решение данной задачи позволит в каждой подсистеме ПС выявить практически не используемые мощности, а следовательно, высвободить часть ранее выделенных капитальных вложений и в итоге повысить рентабельность работы ПС в целом за счет уменьшения себестоимости выпускаемой продукции:

где  d_k  — средняя величина дохода, получаемого при использовании k-го     подразделения ПС в течение единицы времени; g_k   —  средняя величина затрат, производимых в единицу времени при  использовании подразделения ПС R_k.

Задача 4.3. В результате исследования ПС для ее подсистем получено:

r₁ = 1,5;            r₂ = 3;             r₃ = 10;             r₄ = 5;

ρ₁ = 0,4;           ρ₂ = 0,7;          ρ₃ = 0,6;           ρ₄ = 0,6;

v₁ = 10;            v₂ = 20;            v₃ = 15;           v₄ = 30 (часов).

Требуется определить среднее время пребывания одной работы в ПС (с момента поступления в ПС  задания на ее выполнение до момента получения ее заказчиком), среднее количество работ, одновременно находящихся в очереди на выполнение в каждой подсистеме, и среднее  количество всех работ, одновременно находящихся в ПС.

Решение.  Согласно формулам (4.2) – (4.9) имеем:

ü среднее время ожидания в очереди в R_k ПС

ω₁ = 6,6;            ω₂ = 46,6;          ω₃ = 1,5;           ω₄ = 45 (часов);

ü среднее время пребывания каждой работы в ПС

u₁ = 16,6;        u₂ = 66,6;        u₃ = 30;         u₄ = 75;        u = 899,7 (часов);

ü среднюю производительность R_k ПС

x₁ = 0,04;           x₂ = 0,035;          x₃ = 0,033;           x₄ = 0,02;

ü среднее количество работ, находящихся в очереди на выполнение в ПС,

l₁ = 0,264;           l₂ = 1,635;           l₃ = 0,495;            l₄ = 0,9 (работ);

ü среднее количество работ, одновременно находящихся в ПС,

                         N = 5,485 (работ).

Задача 4.4. В ПС выполняются два вида работ – плановые работы, поступающие от заказчиков по хоздоговорам, и работы, поступающие в оперативном режиме от вышестоящих организаций. Известны следующие данные:

ü для работ, поступающих в оперативном режиме, N΄ = 40 (среднее количество работ, одновременно находящихся в ПС и выполняемых в оперативном режиме):

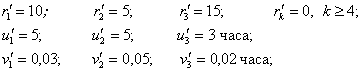
ü для плановых работ

ü коэффициенты загрузки подсистем ПС:

ρ₁ = 0,6;           ρ₂ = 0,9;            ρ₃ = 0,8.

Требуется определить х₀ – производительность ПС по плановым работам.

Решение.  Относительно работ, поступающих в ПС в оперативном режиме, производительность подсистем ПС и ПС в целом будет равна:

                          (4.13)

Ввиду того, что коэффициенты загрузки  характеризуют суммарную загрузку R_k ПС,

Отсюда следует, что

Так как производительность ПС по плановым работам равна

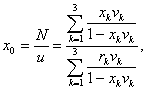
то, используя выписанные выше формулы, окончательно находим

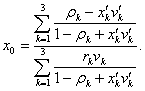                                               (4.14)

Подставляя в формулы (4.13) и (4.14) числовые значения исходных данных, получим

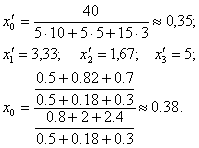
Описанный алгоритм определения производительности ПС относительно плановых работ, имеющих более низкий приоритет, чем работы, поступающие в ПС в оперативном режиме, может быть легко обобщен и на случай, когда в ПС поступают работы трех и более видов (приоритетов).

Задача 4.5. Дана исследуемая система (ПС), состоящая из четырех подсистем, в которую поступает смесь различных работ. В результате наблюдения за работой ПС выявлены следующие исходные данные:

ü среднее время выполнения работ в каждой подсистеме ПС:

                v₁ = 3;          v₂ = 10;          v₃ = 15;          v₄ = 20 (часов);

ü частоты передачи работ из одной системы ПС в другую:

                g₀₁ = 1;

                g₁₀ = 0;        g₁₁ = 0;          g₁₂ = 0.5;       g₁₃ = 0.2;       g₁₄ = 0.3;

                g₂₀ = 0;         g₂₁ = 0;       g₁₂ = 0. 5;        g₂₃ = 0.4;       g₂₄ = 0.6;

                g₃₀ = 0.2;      g₃₁ = 0.2;      g₃₂ = 0.4;       g₁₃ = 0.2;       g₃₄ = 0.2;

                g₄₀ = 0.4;      g₄₁ = 0.1;      g₄₂ = 0;          g₄₃ = 0.5.

Требуется определить минимальное время нахождения работы в ПС u₀ и максимальную производительность ПС u₀.

Решение. Минимальное время нахождения работы в ПС определяется как среднее время нахождения работы в ПС при условии, что  ни к одной ее подсистеме нет очереди из работ, ожидающих начала выполнения, т.е. когда

Поэтому

                                                        (4.15)

Из формулы (4.15) следует, что для определения u₀ достаточно знать только значения коэффициентов посещения  Они находятся из решения балансовых уравнений (4.11). Для заданной ПС система уравнений (4.11) записывается в следующем виде:

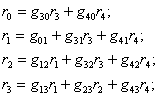
Из первых четырех уравнений выписанной системы уравнений следует:

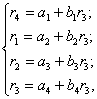                                                  (4.16)

откуда находим

                                      (4.17)

где

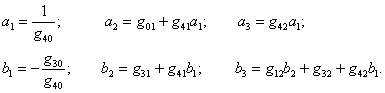
Найдя по формуле (4.17) значение r₃ и подставив его в формулы (4.16), получим:

 r₃ = 1.2;        r₄ = 1.9;        r₁ = 1.27;        r₂ = 1.95.

Используя значения параметров r_k и v_k, по формуле (4.15) определяем

Для определения максимальной производительности исследуемой ПС воспользуемся следующим положением: производительность ПС будет максимальной, если хотя бы у одной ее подсистемы

Так как

то для указанной ПС должно выполняться равенство

Следовательно, для определения  необходимо предварительно найти

а затем по формуле, приведенной выше, вычислить .

Для рассматриваемой задачи получается =0,026 (часа).

Рассмотренные выше типовые задачи не охватывают всего множества задач анализа, которые могут возникнуть в каждой конкретной организации при анализе ее производственной деятельности. Однако они могут успешно использоваться в качестве исходных задач, в результате обобщения которых получаются новые задачи, полнее отвечающие целям исследования. Так, например, задачи 4 и 5 могут быть легко обобщены для случая, когда в ПС выполняются не один тип работ, а два и более с соответствующими им приоритетами в очередности поступления на выполнение.