На рис. 2.17 показана сеть встречного распространения целиком. В режиме нормального функционирования предъявляются входные векторы x и y, и обученная сеть дает на выходе векторы x’ и y’, являющиеся аппроксимациями соответственно для x и y. Векторы x и y предполагаются здесь нормализованными единичными векторами, следовательно, порождаемые на выходе векторы также будут иметь тенденцию быть нормализованными.

В процессе обучения векторы x и y подаются одновременно и как входные векторы сети, и как желаемые выходные сигналы. Вектор x используется для обучения выходов x’, а вектор y – для обучения выходов y’ слоя Гроссберга. Сеть встречного распространения целиком обучается с использованием того же самого метода, который описывался для сети прямого действия. Нейроны Кохонена принимают входные сигналы как от векторов x, так и от векторов y. Но это неотличимо от ситуации, когда имеется один большой вектор, составленный из векторов x и y, и не влияет на алгоритм обучения.

В качестве результирующего получается единичное отображение, при котором предъявление пары входных векторов порождает их копии на выходе. Это не представляется особенно интересным, если не заметить, что предъявление только вектора x (с вектором y, равным нулю) порождает как выходы x’, так и выходы y’. Если F – функция, отображающая x в y’, то сеть аппроксимирует ее. Также, если F обратима, то предъявление только вектора y (приравнивая x нулю) порождает x’. Уникальная способность порождать функцию и обратную к ней делает сеть встречного распространения полезной в ряде приложений.

Рис. 2.17, в отличие от первоначальной конфигурации, не демонстрирует противоток в сети, по которому она получила свое название. Такая форма выбрана потому, что она также иллюстрирует сеть без обратных связей и позволяет обобщить понятия, развитые в предыдущих подразделах.

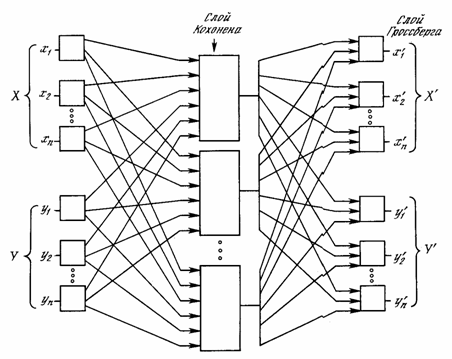
Рис.2.17. Полная сеть встречного распространения