Пример 1. Расстояние (l) между двумя точечными зарядами Q1 = 2 нКл и Q2 = -3 нКл, расположенными в вакууме, равно 20 см. Определить: 1) напряженность (![]() ); 2) потенциал (j) поля, создаваемыми этими зарядами в точке, удаленной от первого заряда на расстоянии r1 = 15 см и от второго заряда на r2 = 10 см.
); 2) потенциал (j) поля, создаваемыми этими зарядами в точке, удаленной от первого заряда на расстоянии r1 = 15 см и от второго заряда на r2 = 10 см.
Дано: l = 20 см = 0,2 м; Q1 = 2 нКл = 2×10-9 Кл; Q2 = -3 нКл = -3×10-9 Кл; r1 = 15 см = 0,15 м; r2 = 10 см = 0,1 м.
 Определить: 1)
Определить: 1) ![]() ; 2) j.
; 2) j.
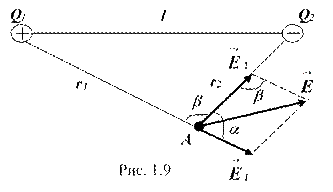
Решение. Согласно принципу суперпозиции имеем: ![]() (рис.1.9).
(рис.1.9).
Напряженности электрического поля, создаваемые в вакууме зарядами Q1 и Q2 , равна:
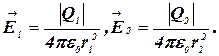 (1)
(1)
Модуль вектора ![]() находится по теореме косинусов:
находится по теореме косинусов:
![]() или
или ![]() , (2)
, (2)
где
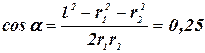 . (3)
. (3)
Подставив (1) и (3) в формулу (2), найдем искомую напряженность в точке А:
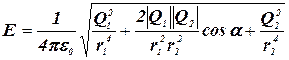 .
.
Согласно принципу суперпозиции, потенциал результирующего поля:
![]() (4)
(4)
где 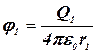 и
и 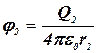 – соответственно потенциалы полей, создаваемых зарядами Q1 и Q2.
– соответственно потенциалы полей, создаваемых зарядами Q1 и Q2.
Подставив последние выражения в (4), найдем:
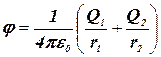 .
.
Вычисляя, получим: 1) ![]() = 3 кВ/м; 2) j = -150 В.
= 3 кВ/м; 2) j = -150 В.
Пример 2. Электрическое поле создается бесконечно длинным цилиндром радиусом R = 7 мм, равномерно заряженным с линейной плотностью t = 15 нКл/м. Определить: 1) напряженность (![]() ) поля в точках, лежащих от оси цилиндра на расстояниях r1 = 5 мм и r2 = 1 см; 2) разность потенциалов между двумя точками этого поля, лежащими на расстоянии r3 = 1 см и r4 = 2 см от поверхности цилиндра, в средней его части.
) поля в точках, лежащих от оси цилиндра на расстояниях r1 = 5 мм и r2 = 1 см; 2) разность потенциалов между двумя точками этого поля, лежащими на расстоянии r3 = 1 см и r4 = 2 см от поверхности цилиндра, в средней его части.
Дано: R = 7 мм = 7×10-3 м; t = 15 нКл/м = 1,5×10-8 Кл/м; r1 = 5 мм = 5×10-3 м;r2 = 1 см =1×10-2 м; r3 = 1 см = 1×10-2 м; r4 = 2 см = 2×10-2 м.
Определить: 1) ![]() ,
, ![]() ; 2)
; 2) ![]() .
.
Решение. Воспользуемся теоремой Гаусса (1.1):
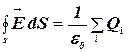 ,
,
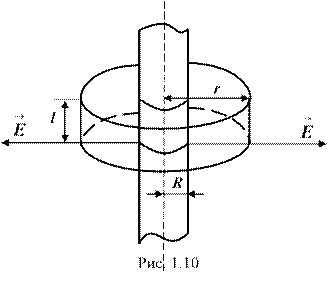 взяв в качестве замкнутой поверхности цилиндр, коаксиальный с заряженным, радиусом r и высотой l (рис. 1.10). Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области
взяв в качестве замкнутой поверхности цилиндр, коаксиальный с заряженным, радиусом r и высотой l (рис. 1.10). Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области ![]() = 0.
= 0.
Поток вектора ![]() сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность поток равен
сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность поток равен ![]() . По теореме Гаусса, при r2 > R
. По теореме Гаусса, при r2 > R
![]() , откуда
, откуда
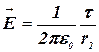 .
.
Так как ![]() , то полученная формула для поля с осевой симметрией запишется в виде:
, то полученная формула для поля с осевой симметрией запишется в виде:
![]() или
или ![]() .
.
Подставив сюда выражение для напряженности поля, создаваемого бесконечно длинным цилиндром ![]() , получим:
, получим:
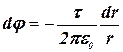 .
.![]()
Проинтегрировав это выражение, найдем искомую разность потенциалов:
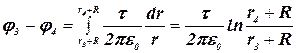 .
.
Вычисляя, получим: 1) ![]() = 0;
= 0; ![]() = 27 кВ/м; 2)
= 27 кВ/м; 2) ![]() = 125 В.
= 125 В.
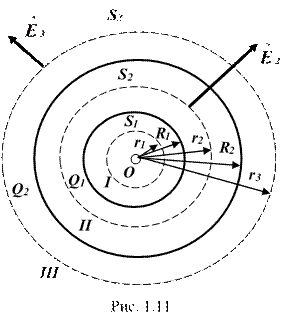
Пример 3. Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут соответственно заряды Q1 = 1 нКл и Q2 = -0,5 нКл. Найти напряженность (![]() ) поля в точках, находящихся от центра сфер на расстояниях: r1 = 5 см, r2 = 9 см, r3 = 15 см. Построить график
) поля в точках, находящихся от центра сфер на расстояниях: r1 = 5 см, r2 = 9 см, r3 = 15 см. Построить график ![]() .
.
Дано: Q1 = 10-9 Кл; Q2 = -0,5×10-9 Кл; r1 = 5 см = 5×10-2 м; r2 = 9 см = 9×10-2 м, r3 = 15 см = 15×10-2 м.
Определить ![]() ;
; ![]() ;
; ![]() .
.
Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 1.11): области I ![]() , области II
, области II ![]() , области III
, области III ![]() .
.
1) Для определения напряженности (![]() ) в области I проведем гауссову поверхность S1 радиусом r1 и воспользуемся теоремой Гаусса:
) в области I проведем гауссову поверхность S1 радиусом r1 и воспользуемся теоремой Гаусса:
![]() ,
,
 так как суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю. Из соображений симметрии имеем:
так как суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю. Из соображений симметрии имеем: ![]() . Следовательно,
. Следовательно, ![]() и
и ![]() (напряженность поля в области I) во всех точках, удовлетворяющих условию
(напряженность поля в области I) во всех точках, удовлетворяющих условию ![]() , будет равна нулю.
, будет равна нулю.
2) В области II гауссову поверхность проведем радиусом r2. В этом случае
![]() ,
,
так как внутри гауссовой поверхности находится только заряд Q1.
Так как ![]() , то
, то ![]() можно вынести за знак интеграла:
можно вынести за знак интеграла:
![]() , или
, или ![]() .
.
Обозначив напряженность ![]() для области II через
для области II через ![]() , получим:
, получим:
![]() ,
,
где ![]() – площадь гауссовой поверхности.
– площадь гауссовой поверхности.
Тогда
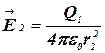 . (1)
. (1)
1) В области III гауссова поверхность проводится радиусом r3. Обозначим напряженность области III через ![]() и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен:
и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен: ![]() . Тогда
. Тогда
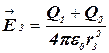 .
.
Заметим, что ![]() ,поэтому это выражение можно переписать в виде:
,поэтому это выражение можно переписать в виде:
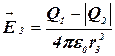 . (2)
. (2)
Убедимся в том, что первая часть равенств (1) и (2) дает единицу напряженности:
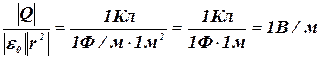 .
.
 Вычисляя, получим:
Вычисляя, получим: ![]() = 0;
= 0; ![]() = 1,11 кВ/м;
= 1,11 кВ/м; ![]() = 200 В/м.
= 200 В/м.
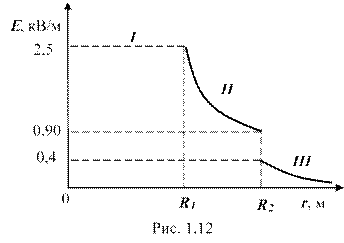
2) Построим график ![]() (рис. 1.12).
(рис. 1.12).
В области I ![]()
![]() = 0.
= 0.
В области II ![]()
![]() изменяется по закону
изменяется по закону ![]() . В точке
. В точке ![]() напряженность равна:
напряженность равна:
![]() = 2,5 кВ/м. В точке
= 2,5 кВ/м. В точке ![]() (r стремится к R2 слева):
(r стремится к R2 слева): ![]() = 0,9 кВ/м.
= 0,9 кВ/м.
В области III ![]()
![]() изменяется по закону
изменяется по закону ![]() , причем в точке
, причем в точке ![]() (r стремится к R2 справа) и напряжённость равна:
(r стремится к R2 справа) и напряжённость равна: ![]() = 0,45 кВ/м.
= 0,45 кВ/м.
 Таким образом, функция
Таким образом, функция ![]() в точках
в точках ![]() и
и ![]() терпит разрыв.
терпит разрыв.
Пример 4. По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью t = 10 нКл/м. Определить напряженность (![]() ) и потенциал (j) электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина (l) нити составляет 1/3 длины окружности и равна 15 см.
) и потенциал (j) электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина (l) нити составляет 1/3 длины окружности и равна 15 см.
Дано: t = 10 нКл/м = 10×10-9 Кл;
l = 15 см = 0,15 м.
Определить: ![]() ; j.
; j.
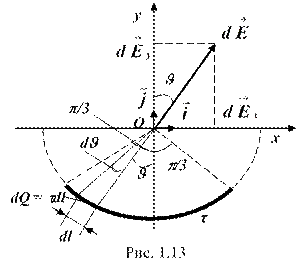
Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Oy была симметрично расположена относительно концов дуги (рис. 1.13). На нити выделим элемент длины dl. Заряд dQ = tdl, находящийся на выделенном участке, можно считать точечным.
Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность (![]() ) поля, создаваемого зарядом dQ:
) поля, создаваемого зарядом dQ:
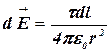 ,
,
где r – модуль радиуса-вектора, направленного от элемента dl к точке, в которой вычисляется напряженность.
Выразим вектор ![]() через проекции
через проекции ![]() и
и ![]() на оси координат:
на оси координат:
![]() ,
,
где ![]() и
и ![]() – единичные векторы направлений (орты).
– единичные векторы направлений (орты).
Напряженность ![]() найдем интегрированием:
найдем интегрированием:
![]() .
.
Интегрирование ведется вдоль дуги длиной l. В силу симметрии ![]() . Тогда
. Тогда
![]() , (1)
, (1)
где ![]() . Так как
. Так как ![]() ,
, ![]() , то
, то
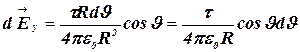 .
.
Подставим выражение ![]() в (1) и, приняв во внимание симметричное расположение дуги относительно оси Oy, пределы интегрирования возьмем от 0 до p/3, а результат удвоим:
в (1) и, приняв во внимание симметричное расположение дуги относительно оси Oy, пределы интегрирования возьмем от 0 до p/3, а результат удвоим:
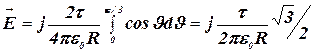 .
.
Выразив радиус R через длину l нити (3l = 2pR), получим:
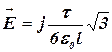 . (2)
. (2)
Из этой формулы видно, что напряженность поля по направлению совпадает с осью Oy.
Найдем потенциал электрического поля в точке О. Сначала найдем потенциал (dj), создаваемый точечным зарядом dQ в точке О:
![]() .
.
Заменим r на R и проведем интегрирование:
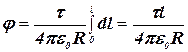 .
.
Так как l = 2pR/3, то
![]() . (3)
. (3)
Вычисляя, получим: ![]() = 2,18 кВ/м; j = 188 В.
= 2,18 кВ/м; j = 188 В.