Для представления в цифровых устройствах чисел, а также другой информации в процессе программирования наряду с привычной для нас десятичной системой счисления широко используются другие системы. Рассмотрим наиболее употребительные позицион­ные системы счисления. Числа в таких системах счисления представляются последователь­ностью цифр (цифр разрядов):

… a₅ a₄ a₃ a₂ a₁ a₀ …

Здесь a₀, a₁, . . . обозначают цифры нулевого, первого и других разрядов числа.

Цифре разряда приписан вес p^k где р — основание системы счисления; k — номер разряда, равный индексу при обозначениях цифр разрядов. Так, приведенная выше запись означает следующее количество:

N = …+  a₅×p⁵ +  a₄×p⁴ +  a₃×p³ +  a₂×p² +  a₁×p¹ +  a₀×p⁰ + …

Для представления цифр разрядов используется набор из p различных символов. Так, при р = 10 (т. е. в обычной десятичной системе счисления) для записи цифр разрядов используется набор из десяти символов: 0, 1, 2 ….. 9. При этом запись 729324₁₀ (здесь и далее индекс при числе указывает основание системы счисления, в которой представлено число) означает следующее количество:

.

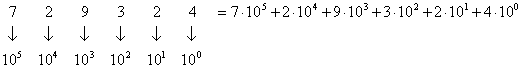Используя такой принцип представления чисел, но выбирая различные значения основания р, можно строить разнообразные системы счисления.

В двоичной системе счисления основание системы счисления р = 2. Таким образом, для записи цифр разрядов требуется набор всего лишь из двух символов, в качестве которых используются 0 и 1. Следовательно, в двоичной системе счисления число представляется последовательностью символов 0 и 1. При этом запись 1011101₂ соответствует в десятичной системе счисления следующему числу:

.

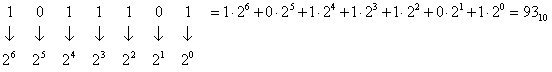В восьмеричной системе счисления основание системы счисления р = 8. Следовательно, для представления цифр разрядов должно использоваться восемь разных символов, в качестве которых выбраны 0, 1, 2,…,7 (заметим, что символы 8 и 9 здесь не используются и в записи чисел встречаться не должны). Например, записи 735460₈ в десятичной системе счисления соответствует следующее число:

,

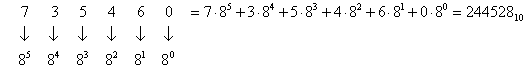т. е. запись 735460₈ означает число, содержащее семь раз по 8⁵ = 32768, три раза по 8⁴ = 4096, пять раз по 8³ = 512, четыре раза по 8² = 64, шесть раз по 8¹ = 8 и ноль раз по 8⁰ = 1.                                                                                                                                                                                  

В шестнадцатеричной системе счисления основание системы счисления р = 16 и для записи цифр разрядов должен использоваться набор из 16 символов: 0, 1,2…..9, А, В, С, D, Е, F. В нем используются 10 арабских цифр, и до требуемых шестнадцати их дополняют шестью начальными буквами латинского алфавита. При этом символу А в десятичной системе счисления соответствует 10, В – 11, С – 12, D – 13, Е – 14, F – 15.

Запись AB9C2F₁₆ соответствует следующему числу в десятичной системе счисления:

,

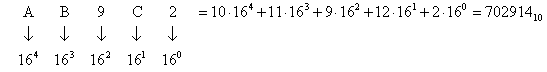Для хранения n-разрядных чисел в цифровой аппаратуре можно использовать устройст­ва, содержащие n элементов, каждый из которых запоминает цифру соответствующего разряда числа. Наиболее просто осуществляется хранение чисел, представленных в двоичной системе счисления. Для запоминания цифры каждого разряда двоичного числа могут исполь­зоваться устройства с двумя устойчивыми состояниями (например, триггеры). Одному из этих устойчивых состояний ставится в соответствие цифра 0, другому – цифра 1.