Основания восьмеричной и шестнадцатеричной систем счисления выражаются целой степенью числа два (8 = 2³, 16 = 2⁴).  Этим объясняется простота преобразования чисел, представленных в этих системах счисления, в двоичную систему счисления и обратно.

Для перевода чисел из восьмеричной системы счисления в двоичную достаточно каждую цифру восьмеричного числа представить трехразрядным двоичным числом. Например:

.

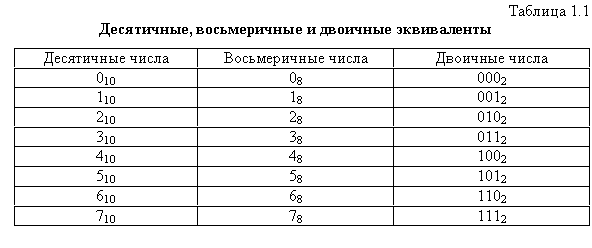
В табл. 1.1 приведены эквиваленты десятичных, восьмеричных и двоичных чисел.

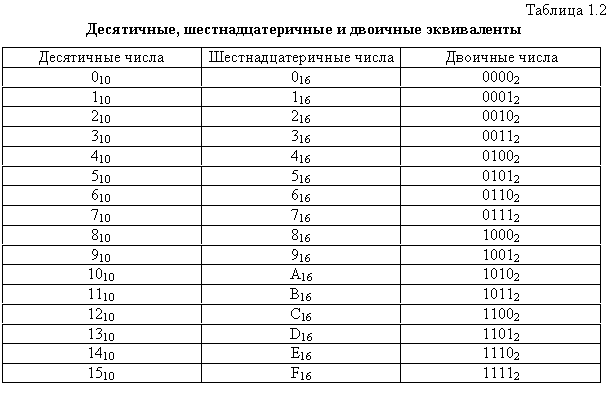
Перевод шестнадцатеричных чисел в двоичную систему счисления достигается пред­ставлением цифр шестнадцатеричного числа четырехразрядными двоичными числами. Например:

.

При обратном переводе чисел из двоичной системы в восьмеричную или шестнадцатеричную систему счисления необходимо разряды двоичного числа разбить на группы по три разряда в случае перевода в восьмеричную систему или на группы по четыре разряда в случае перевода в шестнадцатеричную систему счисления. Неполные крайние группы дополняются нулями. Затем каждая двоичная группа представ­ляется цифрой той системы счисления, в которую переводится число. Например:

;

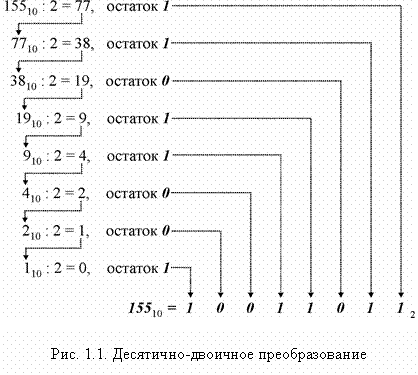
Большую сложность представляет перевод чисел из десятичной системы в двоичную и обратно.  Рассмотрим пример перевода числа 155₁₀ в двоичную систему счисления, процедура перевода приведена на рис. 1.1.

Десятичное число 155 сначала делится на 2, что дает нам частное 77 и остаток 1. Этот остаток становится значением младшего разряда двоичного числа и помещается в крайнюю справа позицию. Затем частное (77) перемещается, как показывает стрелка, и становится следующим делимым. Затем каждое частное последовательно делится на 2 до тех пор, пока не получится частное, равное 0 и остаток, равный 1 (см. рис. 1.1). Последняя строка на рис. 1.1 дает нам результат 155₁₀ = 10011011₂.

Для преобразования десятичных чисел в восьмеричную и шестнадцатеричную системы счисления используют аналогичные алгоритмы.

На рис. 1.2 представлена процедура перевода числа 3336₁₀ в его восьмеричный эквивалент.

В первую очередь число 3336₁₀ разделим на 8, что дает частное 417 и остаток 0₁₀, причем 0₁₀ = 0₈, восьмеричный 0 становится значением младшего разряда восьмеричного числа. Первое частное (417) становится делимым и снова делится на 8 (вторая строка), что дает частное 52 и остаток 1₁₀ = 1₈, который становится второй цифрой восьмеричного числа. В третьей строке частное (52) становится делимым и деление его на 8 дает частное 6 и остаток 4₁₀ =4₈. В четвертой строке частное 6 разделено на 8 с частным 0 и остатком 6₁₀ = 6₈. Теперь счет закончен последним частным 0. Цифра 6₈ становится значением старшего разряда восьмеричного числа, и мы можем видеть на рис. 1.2, что 3336₁₀ = 6410₈.

На рис. 1.3 показана последовательность действий по переводу десятичного числа 15797 в шестнадцатеричное.

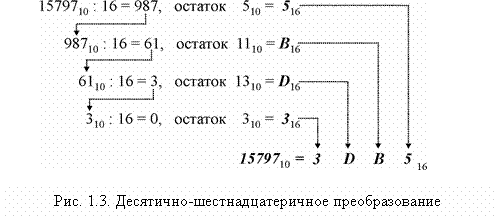
В первой строке 15797₁₀ делится на 16, что дает частное 987₁₀ и остаток 5₁₀, который преобразуется потом в свой шестнадцатеричный эквивалент (5₁₀ = 5₁₆) и становится цифрой младшего разряда шестнадцатеричного числа. Первое частное (987) становится делимым во второй строке и сно­ва делится на 16, что дает частное 61 и остаток 11₁₀ или шестнадцатеричное B. В третьей строке 61 делится на 16, дает частное 3 и остаток 13₁₀ или D₁₆, а в четвертой строке делимое 3 делится на 16, дает частное 0 и остаток 3₁₀ или 3₁₆. Когда частное равно 0 (см. четвертую строку рис. 1.3), преоб­разование заканчивается. 3₁₆ становится цифрой старшего разряда результата, т.е. 3DB5₁₆.