Пример 1. Сила тока в проводнике сопротивлением R = 50 Ом равномерно растет от I0 = 0 до Imax = 3 А за время t = 6 с. Определить выделившееся в проводнике за это время количество теплоты.
Дано: R = 50 Ом; I0 = 0; Imax = 3 А; t = 6 с.
Определить Q.
Решение. Согласно закону Джоуля-Ленца для бесконечно малого промежутка времени имеем:
.
По условию задачи сила тока равномерно растет, т.е. 
, где коэффициент пропорциональности 
. Тогда можно записать:
. (1)
Проинтегрировав (1) и подставив выражение для k, найдем искомое количество теплоты:
.
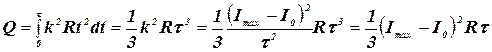Вычисляя, получим: Q = 900 Дж.
Пример 2. Определить внутреннее сопротивление источника тока, если во внешней цепи при силе тока I1 = 4 A развивается мощность Р1 = 10 Вт, а при силе тока I2 = 6 А – мощность Р2 = 12 Вт.
Дано: I1 = 4 A; Р1 = 10 Вт; I2 = 6 А; Р2 = 12 Вт.
Определить r.
Решение. Мощность, развиваемая током, вычисляется по формуле:
и 
, (1)
где R1 и R2 – сопротивления внешней цепи.
Согласно закону Ома:
; 
,
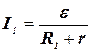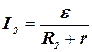где e – ЭДС источника. Решив эти два уравнения относительно r, получим:
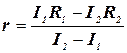. (2)
Выразив I1R1 и I2R2 из уравнений (1) и подставив в выражение (2), найдем искомое внутреннее сопротивление источника тока:
.
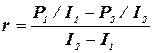Вычисляя, получим: r = 0,25 Ом.